Диаметр площадь: Площадь круга | Онлайн калькулятор
понятие, площадь, формула и таблица соответствия диаметру
Содержание статьи:
Для правильного выбора и организации электролинии необходимо учитывать параметры и нагрузку проводников. Они представляют собой металлическую нить из меди, алюминия, стали, цинка, титана, никеля и обеспечивают передачу тока от его источника до потребителя. У проводников есть поперечное сечение – это фигура, образованная от их рассечения плоскостью поперечного направления. Если его подобрать неправильно, линия выйдет из строя или загорится при скачках напряжения.
Площадь поперечного сечения как электротехническая величина
От поперечного сечения зависит токопроводимость провода
В качестве примера сечения можно рассмотреть распил изделия под углом 90 градусов относительно поперечной оси. Контур фигуры, получившейся в результате, определяется конфигурацией объекта. Кабель имеет вид небольшой трубы, поэтому при распиле выйдет фигура в виде двух окружностей определенной толщины. При поперечном рассечении круглого металлического прута получится форма круга.
При поперечном рассечении круглого металлического прута получится форма круга.
В электротехнике площадь ПС будет значить прямоугольное сечение проводника в отношении к его продольной части. Сечение жил всегда будет круглым. Измерение параметра осуществляется в мм2.
Начинающие электрики могут перепутать диаметр и сечение элементов. Чтобы определить, какая площадь сечения у жилы, понадобиться учесть его круглую форму и воспользоваться формулой:
S = πхR2, где:
- S – площадь круга;
- π – постоянная величина 3,14;
- R – радиус круга.
Если известен показатель площади, легко найти удельное сопротивление материала изготовления и длину провода. Далее вычисляется сопротивление тока.
Для удобства расчетов начальная формула преобразуется:
- Радиус – это ½ диаметра.
- Для вычисления площади π умножается на D (диаметр), разделенный на 4, или 0,8 умножается на 2 диаметра.
При вычислениях используют показатель диаметра, поскольку его неправильный подбор может вызвать перегрев и воспламенение кабеля.
Цели расчета
Поперечное сечение проводов для освещения
Рассчитывать параметры площади сечения проводника необходимо с несколькими целями:
- получение необходимого количества электричества для запитки бытовых приборов;
- исключение переплат за неиспользуемый энергоноситель;
- безопасность проводки и предотвращение возгораний;
- возможность подключения высокомощной техники к сети;
- предотвращение оплавления изоляционного слоя и коротких замыканий;
- правильная организация осветительной системы.
Оптимальное сечение провода для освещения – 1,5 мм2 для линии, 4-6 мм2 на вводе.
Соотношение диаметра кабеля с площадью его сечения
Определение посредством формулы площади поперечного сечения проводников занимает длительное время. В некоторых случаях уместно использовать данные из таблицы. Поскольку для организации современной проводки применяется медный кабель, в таблицу вносятся параметры:
- диаметр;
- сечение в соответствии с показателем диаметра;
- предельная мощность нагрузки проводников в сетях с напряжением 220 и 380 В.

| Диаметр жилы, мм | Параметры сечения, мм2 | Сила тока, А | Мощность медного проводника, кВт | |
| Сеть 220 В | Сеть 380 В | |||
| 1,12 | 1 | 14 | 3 | 5,3 |
| 1,38 | 1,5 | 15 | 3,3 | 5,7 |
| 1,59 | 2 | 19 | 4,1 | 7,2 |
| 1,78 | 2,5 | 21 | 4,6 | 7,9 |
| 2,26 | 4 | 27 | 5,9 | 10 |
| 2,76 | 6 | 34 | 7,7 | 12 |
| 3,57 | 10 | 50 | 11 | 19 |
Посмотрев данные в соответствующих колонках, можно узнать нужные параметры для электролинии жилого здания или производственного объекта.
Расчет сечения многожильного проводника
Многожильный провод представляет собой несколько отдельных жил. Расчет его сечения осуществляется следующим образом:
Расчет его сечения осуществляется следующим образом:
- Находится показатель площади сечения у одной жилы.
- Пересчитываются кабельные жилы.
- Количество умножается на поперечное сечение одной жилы.
При подключении многожильного проводника его концы обжимаются специальной гильзой с использованием обжимных клещей.
Особенности самостоятельного расчета
Самостоятельное вычисление продольного сечения выполняется на жиле без изоляционного покрытия. Кусочек изоляции можно отодвинуть или снять на отрезке, приобретенном специально для тестирования. Вначале понадобится определить диаметр и по нему найти сечение. Для работ используется несколько методик.
При помощи штангенциркуля
Способ оправдан, если будут измеряться параметры усеченного, или бракованного кабеля. К примеру, ВВГ может обозначаться как 3х2,5, но фактически быть 3х21. Вычисления производятся так:
- С проводника снимается изоляционное покрытие.

- Диаметр замеряется штангенциркулем. Понадобится расположить провод между ножками инструмента и посмотреть на обозначения шкалы. Целая величина находится сверху, десятичная – снизу.
- На основании формулы поиска площади круга S = π (D/2)2 или ее упрощенного варианта S = 0,8 D² определяется поперечное сечение.
- Диаметр равен 1,78 мм. Подставляя величину в выражение и округлив результат до сотых, получается 2,79 мм2.
Для бытовых целей понадобятся проводники с сечением 0,75; 1,5; 2,5 и 4 мм2.
С использованием линейки и карандаша
Вычисление ПС с помощью линейки и карандаша
При отсутствии специального измерителя можно воспользоваться карандашом и линейкой. Операции выполняются с тестовым образом:
- Зачищается от изоляционного слоя участок, равный 5-10 см.
- Получившаяся проволока наматывается на карандаш. Полные витки укладываются плотно, пространства между ними быть не должно, «хвостики» направляются вверх или вниз.

- В конечном итоге должно получиться определенное число витков, их требуется посчитать.
- Намотка прикладывается к линейке так, чтобы нулевое деление совпадало с первой намоткой.
- Замеряется длина отрезка и делится на количество витков. Получившаяся величина – диаметр.
- Например, получилось 11 витков, которые занимают 7,5 мм. При делении 7,5 на 11 выходит 0,68 мм – диаметр кабеля. Сечение можно найти по формуле.
Точность вычислений определяется плотностью и длиной намотки.
Таблица соответствия диаметра проводов и площади их сечения
Если нет возможности пройти тестирование диаметра или сделать вычисление при покупке, допускается использовать таблицу. Данные можно сфотографировать, распечатать или переписать, а затем применять, чтобы найти нормативный или популярный размер жилы.
| Диаметр кабеля, мм | Сечение проводника, мм2 |
| 0,8 | 0,5 |
| 0,98 | 0,75 |
| 1,13 | 1 |
| 1,38 | 1,5 |
| 1,6 | 2 |
| 1,78 | 2,5 |
| 2,26 | 4 |
| 2,76 | 6 |
| 3,57 | 10 |
При покупке электрокабеля понадобится посмотреть параметры на этикетке.
Чаще всего диаметр кабеля меньше, чем заявлен на упаковке. У пользователя два варианта – применять другой или выбрать с большей площадью сечения кабель по диаметру. Выбрав второй, понадобится проверить изоляцию. Если она не сплошная, тонкая, разная по толщине, остановитесь на продукции другого изготовителя.
Определение сечения проводника на вводе
Уточнить номинальные показатели можно в компании Энергосбыта или документации к товару. К примеру, номинал автомата на вводе составляет 25 А, мощность потребления – 5 кВт, сеть однофазная, на 220 В.
Подбор сечения осуществляется так, чтобы допустимый ток жил за длительный период был больше номинала автомата. Например, в доме на ввод пущен медный трехжильный проводник ВВГнг, уложенный открытым способом.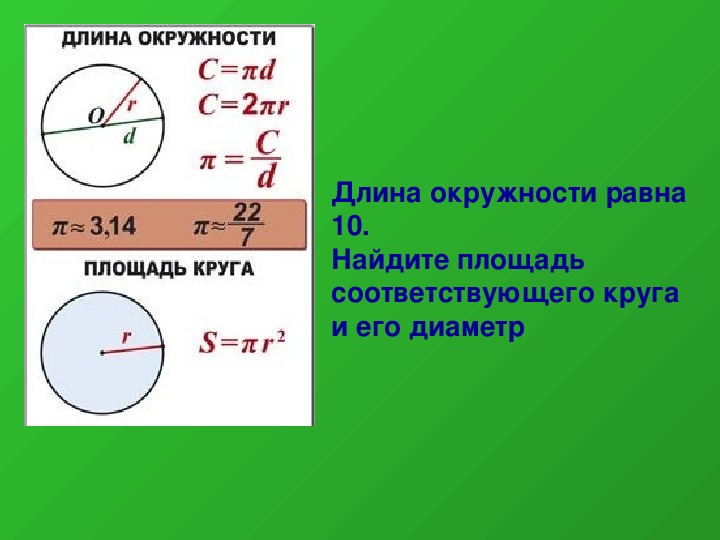
После этого высчитывается показатель условного тока отключения для автомата с номиналом 25 А: 1,45х25=36,25 А. У кабеля с площадью сечения 4 мм2 параметры длительно допустимого тока 35 А, условного – 36,25 А. В данном случае лучше взять вводный проводник из меди сечением 6 мм2 и допустимым предельным током 42 А.
Вычисление сечения провода для линии розеток
Сечение кабелей для домашних электроустановок
Каждый электроприбор имеет показатели собственной мощности. Они замеряются в Ваттах и указываются в паспорте либо на наклейке на корпусе. Примером поиска сечения будет линия запитки для стиральной машины мощностью 2,4 кВт. При расчетах учитывается:
- материал провода и способ укладки – трехжильный ВВГнг-кабель из меди, спрятанный в стене;
- особенности сечения – оптимальная величина составляет 1,5 мм2, т.е. понадобится кабель 3х1,5;
- использование розетки. Если подключается только машинка-автомат, характеристик будет достаточно;
- система защиты – автомат, номинальный ток которого 10 А.

Для двойных розеток применяется кабель из меди с сечением 2,5 мм2 и автомат номиналом 16 А.
Подбор сечения для трехфазной линии 380 В с несколькими приборами
Подключение нескольких видов бытовой техники к трехфазной линии предусматривает протекание потребляемого тока по трем жилам. В каждом из них будет меньшая величина, чем в двухжильном. На основании данного явления в трехфазной сети допускается применять кабель с меньшим сечением.
К примеру, в доме устанавливается генератор с мощностью 20 кВт и суммарной мощностью по трем фазам 52 А. На основании значений таблицы выйдет, что оптимальное сечение кабеля – 8,4 мм2. На основании формулы высчитывается фактическое сечение: 8,4/1,75=4,8 мм2. Чтобы подсоединить генератор мощностью 20 кВт на трехфазную сеть 380 В необходим медный проводник, сечение каждой жилы которого 4,8 мм2.
Сечение проводов в домах старой застройки и предельная нагрузка
В многоэтажках советского периода используется алюминиевая проводка. С учетом правильного соединения узлов в распредкоробе, качества изоляции и надежности контактов соединения она прослужит от 10 до 30 лет.
С учетом правильного соединения узлов в распредкоробе, качества изоляции и надежности контактов соединения она прослужит от 10 до 30 лет.
При необходимости подключения техники с большой энергоемкостью в домах с проводкой из алюминия на основе мощности потребления подбирается сечение и диаметр жил. Все данные указаны в таблице.
| Ток, А | Максимальная мощность, ВА | Диаметр кабеля, мм | Сечение кабеля, мм2 |
| 14 | 3000 | 1,6 | 2 |
| 16 | 3500 | 1,8 | 2,5 |
| 18 | 4000 | 2 | 3 |
| 21 | 4600 | 2,3 | 4 |
| 24 | 5300 | 2,5 | 5 |
| 26 | 5700 | 2,7 | 6 |
| 31 | 6800 | 3,2 | 8 |
| 38 | 8400 | 3,6 | 10 |
Какой кабель выбрать для квартирной проводки
Несмотря на дешевизну алюминиевых проводников, от их применения лучше отказаться. Причина – низкая надежность контактов, через которые будут проходить токи. Второй повод – несоответствие сечения провода мощности современной бытовой техники. Кабель из меди отличается надежностью, длительным сроком эксплуатации.
Причина – низкая надежность контактов, через которые будут проходить токи. Второй повод – несоответствие сечения провода мощности современной бытовой техники. Кабель из меди отличается надежностью, длительным сроком эксплуатации.
В квартирах и домах допускается использовать провод с маркировкой:
- ПУНП – плоский проводник с медными жилами в ПВХ-оболочке. Рассчитан на напряжение номиналом 250 В при частоте 50 Гц.
- ВВГ/ВВГнг – плоские кабели из меди с двойным ПВХ-покрытием. Применяются внутри и снаружи сооружений, не подвержены возгоранию. Бывают с 2-мя, 3-мя и 4-мя жилами.
- NYM – провод из меди для внутренней одиночной линии. Имеет изоляционную ПВХ-оболочку и наружное покрытие, жилы с заземлением и без него.
При выборе количества жил понадобится учесть способность токопроводимости на единицу сечения. В данном случае квартирную сеть лучше сделать из одножильного провода, толщина которого больше. Многожильные элементы можно изгибать многократно, подсоединять на них электроприборы. Качественным будет только кабель с тонкими жилами.
Качественным будет только кабель с тонкими жилами.
Правильное сечение проводников, учет мощности оборудования и типа сети – важные факторы при организации электролинии. Диаметр кабеля можно несколькими способами вычислить самостоятельно. Основываясь на этих показаниях, легко определить сечение жил по формулам или с помощью таблицы.
Площадь круга и его частей. Визуальный гид (ЕГЭ — 2021)
P.S. Последний бесценный совет 🙂
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут.
Почему?
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ОГЭ или ЕГЭ, для поступления в 10 класс или в институт на бюджет и, самое главное, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы быть наверняка лучше других на ОГЭ или ЕГЭ и быть в конечном итоге… более счастливым?
Набить руку, решая задачи.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можешь воспользоваться нашим сборником задач с подробным разбором, и мы их всячески рекомендуем, потому что они разбиты по темам, по типам и даже собраны в целую программу подготовки.
Если решишь набить руку с помощью наших задач, зайди на сайт 100gia и приобрети одну из программ.
А еще можешь зарегистрироваться и получить доступ к огромному количеству бесплатных материалов, видеоуроков, тестов.
После регистрации ты сможешь:
Бонус: информатика и физика.
И в заключение…
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
Только не останавливайся на теории.
“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Квадратный метр это сколько: как измерить квадратуру комнаты самостоятельно
При проведении ремонтных работ возникает вопрос: квадратный метр – это сколько необходимо материалов, чтобы его покрыть.
Чтобы не потратить лишние деньги, лучше для начала произвести расчет квадратных метров комнаты и только потом отправляться в магазин с конкретными требованиями.
На упаковках с красками, штукатуркой, грунтовкой обязательно обозначено, на какой размер помещения рассчитано данное количество смеси.
Главный вопрос – сколько необходимо упаковок или банок, чтобы хватило на площадь стен или пола.
Что такое квадратный метр
Для начала надо определиться, что из себя представляет квадратный метр. Люди, которые плохо учили в школе математику, все равно рано или поздно сталкиваются с проблемой подсчета количества строительных материалов. Поэтому квадратный метр – основная точка отсчета при определении площади помещения.
Поэтому квадратный метр – основная точка отсчета при определении площади помещения.
Если нарисовать квадрат (это геометрическая фигура с одинаковыми сторонами), и сторона будет равна 100 см, то при умножении на 100 получим число 10000 см. это означает, что размер данной фигуры 10000 см2. Можно проще. Посчитать в метрах: 100 см – это 1 м. Применяем формулу подсчета площади – перемножаем две стороны, то есть 1 умножаем на 1, получаем 1 м. Значит, размер квадрата 1 кв.м.
Инструменты для подсчета квадратных метров
Для вычислений необходимо подготовить калькулятор.
Если его нет, тогда таблицу умножения на обычной тетради для первоклассника.
Если стены имеют не 2, не 3 метра, а, например 2,5 метра, то лучше все-таки калькулятор. Это чересчур сложная нагрузка для мозга, который не привык работать с цифрами.
Желательно иметь под руками листок бумаги и ручку для записи.
Измерять необходимо рулеткой или сантиметром.
Формула подсчета квадратных метров
Чтобы рассчитать площадь, необходимо применить формулу квадратного метра А X B, где число А – это длина одной стороны, а число В – длина второй стороны. Они могут быть одинаковы, если форма пола или стены квадратная.
Чаще всего она не квадратная, а прямоугольная, то есть число А будет иметь одно значение, а число В – другое. Их необходимо будет перемножить в уме, или по таблице умножения, или на калькуляторе. И полученное число будет площадью, которую надо будет покрывать краской или еще чем-нибудь.
Это интересно! Иногда нужно знать как правильно высчитываются размеры. Сколько же дюймов в мм? Об этом можно прочесть в нашей статье.
Бывает, что форма пола не стандартная, а, например, трапециевидная. Тогда сложнее, особенно тем людям, кто не знает, что такое треугольник (такое тоже есть в природе). Чтобы рассчитать размер трапеции, необходимо посчитать сначала площадь прямоугольника в середине, потом величину каждого треугольника по бокам, потом эти три числа сложить. Не легче ли сразу позвать бригаду рабочих? Пускай они думают, как рассчитать квадратные метры комнаты.
Важно! Если на этом этапе возникло непонимание, то лучше сразу позвать учителя математики и попросить подсчитать, сколько кв. метров имеет комната.
Площадь пола или потолка
Потолка и пол в обычной квартире одинаковые. Как посчитать квадратные метры? Очень просто. Если помещение мансардное, тогда потолка там нет – есть только пол и стены.Этап № 1. Измерить длину комнаты и записать полученное число на бумаге. Если число целое, тогда пишем просто цифру. Например, 5 (м). Если число больше 5, но меньше 6, тогда придется вспомнить десятичные дроби и написать, к примеру, 5,5 (м).
Этап № 2. Измерить ширину комнаты и записать аналогично. К примеру – 3м.
Этап № 3. Теперь необходимо перемножить эти два числа. Пример: 5 x 3 = 15м. Итак, площадь пола – 15 кв. м. Следовательно, размер потолка также будет равняться 15 кв. м. Записать это число отдельно и обвести ручкой.
Площадь сплошной стены
Как вычислить квадратуру сплошной стены? Так же, как мы измеряли пол или потолок. Алгоритм действий тот же, что и при подсчете размера пола:
- измерить длину стены и записать;
- измерить высоту;
- перемножить два числа – полученный результат и будет площадью в квадратных метрах.
Пример: высота 2,20 м, длина 7м. 7 x 2,2 = 15,4 м. Площадь стены – 15,4 кв. м.
Как посчитать квадратные метры стены с окном
Сложнее будет иметь дело со стеной, на которой расположено окно.В таком случае надо отдельно высчитать размер стены, отдельно – размер окна. Потом из большей площади вычесть меньшую. Получится число метров квадратных, которое необходимо будет покрыть краской или штукатуркой.
Алгоритм действий:
- По уже пройденному сценарию высчитать размер стены. Пускай будет уже известное число – 15,4 м2.
- Далее измерить высоту и длину окна. Перемножить числа. К примеру: длина 1,5 м, высота 1,2 м. Если умножить, то получится 1,8. Значит, площадь окна 1,8 кв. м.
- Берем площадь стены и вычитаем из нее размер окна: 15,4 – 1,8 = 13,6. Площадь, которую необходимо будет привести в порядок, – 13,6 кв. м.
Важно! Цифры, которые получаются при подсчетах, обязательно записывать и обводить ручкой, чтобы не потеряться в собственных расчетах.
Как посчитать квадратные метры стены с дверью
Похожие действия необходимо производить, когда требуется высчитать квадратные метры стены с дверью. Если дверь с математической точки зрения простой прямоугольник, то вычисляем ее площадь по обычной формуле А X В. То есть надо измерить высоту и длину, далее числа перемножить и получится размер двери.
Далее из площади стены вычитаем размер двери и получаем квадратуру, на которую необходимо будет покупать отделочные материалы. Если предыдущий хозяин квартиры сделал дверь с аркой, то здесь без вычисления размера круга никак не обойтись.
Измеряем площадь сложных фигур
Круг и треугольник – сложные фигуры для самостоятельного вычисления. Как измерить квадратные метры окружности, если нет математического или инженерного образования? Опять-таки по формуле.
Как измерить размер окружности
Существует формула вычисления площади круга. Есть такое постоянное число – отношение длины окружности к ее диаметру. Оно одинаково для всех размеров круга. Называется оно пи и равняется 3,14. Вот это число и используют при подсчетах.Этап № 1. Замеряем диаметр (это линия, которая проходит через центр круга от одного края окружности к другому). Пускай диаметр будет равняться 3 м. Далее находим радиус – это половина длины диаметра. То есть 1,5 м. Записываем радиус на бумагу.
Этап № 2. Производим расчеты по формуле S = ПR2, где S – это площадь круга, П – постоянное число, а R – радиус окружности. Получается 3,14 x (1,5 x 1,5) = 7, 065. Площадь данного круга – 7,065 кв. м.
Но это площадь целого круга. Арка над дверью – это половина круга. Значит, еще нужно разделить данное число на два и далее прибавить к прямоугольной площади двери. 7,065 : 2 = 3,53 м2.
Как измерить площадь треугольника
Если предыдущий хозяин квартиры был математик, то он вполне мог сделать на потолке треугольные фигуры, которые приходится реставрировать и выделять другим цветом или штукатуркой. Придется считать, чтобы не переплачивать.
Расчет метра квадратного в треугольной фигуре начинается с внимательного осмотра этой фигуры.
Необходимо найти основание треугольника, то есть линию, на которую опираются две других (как крыша на доме). Далее провести линию из противоположной верхушки к основанию. Эти два числа записать.
- Этап № 1. Разделить основание треугольника на 2 и записать. Это число пригодится в недалеком будущем. Измерить высоту и тоже записать.
- Этап № 2. Произвести расчет м2 фигуры. Для этого необходимо использовать формулу: S = 0,5аh, где S – площадь треугольника, а – основание, а h – высота. Пример: основание 3 м, высота 2,5 м. Итого: 0,5 x 3 x 2,5 = 3,75. Размер треугольника – 3,75 м2. Записать, чтобы не забыть.
Советы и рекомендации
Таким образом можно высчитать площадь всей квартиры и расписать, что и каким цветом красить. Размеры всех стен и потолка сложить – получится число, на которое надо будет ориентироваться при покупке стройматериалов.
Совет! При расчетах лучше пригласить еще одного человека в помощь. Одна голова хорошо, а две надежнее.
Дело за малым – пойти в магазин и купить материалы. Здесь еще придется считать, так как не все упаковки предназначены для больших помещений. К примеру, размер потолка на кухне 3 x 3. Сколько квадратных метров штукатурки понадобится, если одной упаковкой можно покрыть 3 кв. м? Считаем: размер потолка 9 кв. м. Одна упаковка уходит на 3 кв. м. Следовательно, на весь потолок необходимо 3 пачки.
Если на упаковке написано, что расход на 12 квадратных метров, это означает, сколько материала надо, чтобы покрыть стену размером 3 x 4 м.
Или другой пример. Стена в квартире 6 на 4. Сколько квадратных метров необходимо закрасить? Умножаем 6 на 4, получаем 24 квадратных метра. Это сколько нужно банок краски по 3 л, если каждая банка расходуется на 6 кв. м? Считаем: 24 делим на 6. Получается 4. Значит, необходимо купить 4 трехлитровых банки краски для покрытия всей стены.
Для ремонтных работ всегда лучше взять немного больше материалов, чтобы потом не идти лишний раз в магазин. В будущем, если придется что-то подкрасить или подбелить, остатки материалов могут здорово выручить.
Видео по теме: квадратные метры в помещении
Площадь — Википедия. Что такое Площадь
Пло́щадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры[1], неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже). Фигуры с одинаковой площадью называются равновеликими.
Общий метод вычисления площади геометрических фигур предоставило интегральное исчисление. Обобщением понятия площади стала теория меры множества, пригодная для более широкого класса геометрических объектов.
Для приближенного вычисления площади на практике используют палетку или специальный измерительный прибор — планиметр.
Определение понятия площади
Множество измеримо по Жордану, если внутренняя мера Жордана равна внешней мере ЖорданаПлощадь — функция, которая обладает следующими свойствами[2][1]:
- Положительность, то есть площадь неотрицательна;
- Аддитивность, то есть площадь фигуры равна сумме площадей составляющих её фигур без общих внутренних точек;
- Инвариантность, то есть площади конгруэнтных фигур равны;
- Нормированность, то есть площадь единичного квадрата равна 1.
Из данного определения площади следует её монотонность, то есть площадь части фигуры меньше площади всей фигуры[2].
Первоначально определение площади было сформулировано для многоугольников, затем оно было расширено на квадрируемые фигуры. Квадрируемой называется такая фигура, которую можно вписать в многоугольник и в которую можно вписать многоугольник, причём площади обоих многоугольников отличаются на произвольно малую величину. Такие фигуры называются также измеримыми по Жордану[1]. Для фигур на плоскости, не состоящих из целого количества единичных квадратов, площадь определяется с помощью предельного перехода; при этом требуется, чтобы как фигура, так и её граница были кусочно-гладкими[3]. Существуют неквадрируемые плоские фигуры[1]. Предложенное выше аксиоматическое определение площади в случае плоских фигур обычно дополняют конструктивным, при котором с помощью палетки осуществляется собственно вычисление площади. При этом для более точных вычислений на последующих шагах используют палетки, у которых длина стороны квадрата в десять раз меньше длины у предыдущей палетки[4].
Площадь квадрируемой плоской фигуры существует и единственна. Понятие площади, распространённое на более общие множества, привело к определению множеств, измеримых по Лебегу, которыми занимается теория меры. В дальнейшем возникают более общие классы, для которых свойства площади не гарантируют её единственность[1].
Под площадью в обобщённом смысле понимают численную характеристику k-мерной поверхности в n-мерном пространстве (евклидовом или римановом), в частности, характеристику двумерной поверхности в трёхмерном пространстве[1].
Общий метод определения площади
Площадь плоской фигуры
На практике чаще всего требуется определить площадь ограниченной фигуры с кусочно-гладкой границей. Математический анализ предлагает универсальный метод решения подобных задач.
Декартовы координаты
Определённый интеграл как площадь фигуры Площадь между графиками двух функций равна разности интегралов от этих функций в одинаковых пределах интегрированияПлощадь, заключённая между графиком непрерывной функции на интервале [a,b]{\displaystyle [a,b]} и горизонтальной осью, может быть вычислена как определённый интеграл от этой функции:
- S=∫abf(x)dx{\displaystyle S=\int \limits _{a}^{b}f(x)\,dx}
Площадь, заключённая между графиками двух непрерывных функций f(x),g(x){\displaystyle f(x),\,g(x)} на интервале [a,b]{\displaystyle [a,b]} находится как разность определённых интегралов от этих функций:
S=∫ab|f(x)−g(x)|dx{\displaystyle S=\int \limits _{a}^{b}\left|f(x)-g(x)\right|\,dx}
Полярные координаты
В полярных координатах: площадь, ограниченная графиком функции r=r(θ){\displaystyle r=r(\theta )} и лучами
преобразовать диаметр в миллиметры (мм, диаметр проволоки) к площади сечения в круглых милах (Площадь сечения провода)
Американский калибр проводов — это стандарт, используемый в Соединенных Штатах с 1857 года для меди, алюминия, золота, серебра и т. Д. Он также известен как калибр Brown & Sharpe . Чем больше номер калибра, тем меньше диаметр проволоки. Провода толще 0 калибра обозначаются как 00 (или 2/0 ), 000 (или 3/0 ) и т. Д.
Washburn & Moen Калибр для стальной проволоки используется в США для производства стали. Он также известен как US Steel Wire или Roebling Gauge .
Британский стандартный калибр для проволоки больше не пользуется популярностью, но все еще используется для измерения струн гитары. Он также известен как Imperial Wire Gauge или British Standard Gauge . SVG определяет только датчики от 7/0 до 50 .
Birmingham Wire Gauge теперь является устаревшим.Его размеры не прогрессируют ни геометрически, ни арифметически и, следовательно, не имеют определенного отношения друг к другу. B.W.G определяет размеры от 5/0 до 36 .
IEC 60228 — это международный стандарт, который, помимо прочего, определяет набор стандартных проводов. Размеры проводов в этом стандарте обозначаются по их площади поперечного сечения, выраженной в мм². ГОСТ 22483-2012 — это немного измененная версия IEC 60228 , которая используется в России, Беларуси, Кыргызстане и Узбекистане.Он добавляет несколько меньших размеров проводов к международному стандарту.
Если площадь сечения или диаметр провода не соответствует калибру, используется ближайший из них, а разница в площади отображается в процентах.
Единицы: Американский калибр проводов, AWG / Washburn & Moen Gauge для стальной проволоки, W&M / Британский стандартный калибр проводов, SWG / Калибр для железной проволоки Бирмингема или Стабса, B.W.G. / Калибр стальной проволоки заглушек / IEC 60228: 2004 Стандартное поперечное сечение провода (мм²) / Сечение провода стандартное ГОСТ 22483-2012. (мм²)
Радиус круга для данной площади Калькулятор
- Цель использования
- Определение площади башни 100 кв. Футов в Dungeons and Dragons.
[1] 2020/10/04 10:21 Мужчина / 30-летний уровень / Другое / Очень /
- Цель использования
- Рассчитайте размер пиццы, если вы превратили две 9-дюймовые пиццы в одну пиццу .
[2] 2020/05/18 06:36 Мужской / 50-летний уровень / Пенсионер / Очень /
- Цель использования
- определение радиуса круга на основе площадь
[3] 2020/04/25 00:20 Женский / 20-летний уровень / Старшая школа / Университет / аспирант / Очень /
- Цель использования
- edulastic…..
- Комментарий / Запрос
- что происходит
[4] 2020/03/31 12:29 Мужской / До 20 лет / Высшая школа / Вуз / аспирант / Маленький /
- Цель используйте
- Найдите радиус «локальной» территории на основе квадратного километра муниципальных властей
[5] 2020.03.03 13:48 Женский / 30-летний уровень / Учитель / Исследователь / Полезно /
- Цель использования
- Получение дополнительной информации о покрытии интернет-маршрутизатора
[6] 2020/02/27 23:55 Женщина / уровень 30 лет / Офисный работник / Государственный служащий / Очень /
- Цель использования
- Назначение
- Комментарий / Запрос
- ничего
[7] 30.01.2020 21:01 Мужчина / До 20 лет / Начальная школа / Ученик средней школы / Очень /
- Цель использования
- I я художник.Я использую этот сайт для исследования геометрических форм. Это ОЧЕНЬ полезно! Спасибо.
[8] 2019/11/10 23:33 Мужской / 40-летний уровень / Самозанятые лица / Очень /
- Цель использования
- Чтобы получить знания и как найти радиус, когда дана только площадь круга
- Комментарий / запрос
- Пожалуйста, помогите мне рассчитать радиус с заданной площадью
[9] 2019/10/21 22:47 Женский / Моложе 20 лет / Высшая школа / Университет / аспирант / Полезный /
- Цель использования
- для ixl
- Комментарий / запрос
- пожалуйста, при использовании площади используйте окружность
[10] 2019/05/16 07:57 Женский / до 20 лет / начальная школа / младший старшеклассник / Совсем нет /
AWG в мм / мм2 | Преобразование размера в мм
Американский калибр проволоки (AWG) в мм и мм 2 Калькулятор преобразования, таблица и способ преобразования.
Калькулятор преобразованияAWG в мм
* Значения диаметра и площади округлены до ближайшего значения AWG.
Калькулятор калибра провода ►
AWG к калькулятору общей площади
Как преобразовать AWG в мм
При вычислении AWG по диаметру или площади поперечного сечения диаметр и площадь поперечного сечения округляются до ближайших значений, эквивалентных AWG.
Расчет диаметра проволоки
Проволока калибра n, диаметр d n в миллиметрах (мм) равно 0.127 мм умножить на 92 в степени 36 минус число n, разделенное на 39:
d n (мм) = 0,127 мм × 92 (36- n ) / 39
0,127 мм — диаметр калибра № 36.
Расчет площади поперечного сечения провода
Площадь поперечного сечения провода n-го калибра A n в квадратных миллиметрах (мм 2 ) равно пи, деленному на 4 диаметра квадратной проволоки d в миллиметрах (мм):
A n (мм 2 ) = (π / 4) × d n 2 = 0.012668 мм 2 × 92 (36- n ) /19,5
Таблица преобразованияAWG в мм
| AWG # | Диаметр (мм) | Диаметр (дюйм) | Площадь (мм 2 ) |
|---|---|---|---|
| 0000 (4/0) | 11,6840 | 0,4600 | 107.2193 |
| 000 (3/0) | 10,4049 | 0,4096 | 85.0288 |
| 00 (2/0) | 9.2658 | 0,3648 | 67.4309 |
| 0 (1/0) | 8,2515 | 0,3249 | 53,4751 |
| 1 | 7,3481 | 0,2893 | 42,4077 |
| 2 | 6.5437 | 0,2576 | 33,6308 |
| 3 | 5,8273 | 0,2294 | 26.6705 |
| 4 | 5,1894 | 0,2043 | 21.1506 |
| 5 | 4,6213 | 0,1819 | 16,7732 |
| 6 | 4,1154 | 0,1620 | 13.3018 |
| 7 | 3,6649 | 0,1443 | 10,5488 |
| 8 | 3,2636 | 0,1285 | 8,3656 |
| 9 | 2,9064 | 0,1144 | 6,6342 |
| 10 | 2.5882 | 0,1019 | 5,2612 |
| 11 | 2.3048 | 0,0907 | 4,1723 |
| 12 | 2,0525 | 0,0808 | 3,3088 |
| 13 | 1,8278 | 0,0720 | 2,6240 |
| 14 | 1,6277 | 0,0641 | 2,0809 |
| 15 | 1.4495 | 0,0571 | 1.6502 |
| 16 | 1,2908 | 0,0508 | 1,3087 |
| 17 | 1,1495 | 0,0453 | 1,0378 |
| 18 | 1.0237 | 0,0403 | 0,8230 |
| 19 | 0,9116 | 0,0359 | 0,6527 |
| 20 | 0,8118 | 0,0320 | 0,5176 |
| 21 | 0.7229 | 0,0285 | 0,4105 |
| 22 | 0,6438 | 0,0253 | 0,3255 |
| 23 | 0,5733 | 0,0226 | 0,2582 |
| 24 | 0,5106 | 0,0201 | 0,2047 |
| 25 | 0,4547 | 0,0179 | 0,1624 |
| 26 | 0,4049 | 0,0159 | 0.1288 |
| 27 | 0,3606 | 0,0142 | 0,1021 |
Расчетная область | SkillsYouNeed
Площадь — это мера того, сколько места внутри фигуры. Вычисление площади формы или поверхности может быть полезно в повседневной жизни — например, вам может потребоваться знать, сколько краски нужно купить для покрытия стены или сколько семян травы вам нужно, чтобы засеять газон.
На этой странице описаны основные сведения, которые необходимо знать для понимания и расчета площадей общих форм, включая квадраты и прямоугольники, треугольники и круги.
Расчет площади методом сетки
Когда фигура рисуется на масштабированной сетке, вы можете найти площадь, подсчитав количество квадратов сетки внутри фигуры.
В этом примере внутри прямоугольника 10 квадратов сетки.
Чтобы найти значение площади с помощью метода сетки, нам нужно знать размер, который представляет квадрат сетки.
В этом примере используются сантиметры, но тот же метод применяется к любой единице длины или расстояния.Вы можете, например, использовать дюймы, метры, мили, футы и т. Д.
В этом примере каждый квадрат сетки имеет ширину 1 см и высоту 1 см. Другими словами, каждый квадрат сетки равен одному квадратному сантиметру.
Подсчитайте квадраты сетки внутри большого квадрата, чтобы найти его площадь.
Есть 16 маленьких квадратов, поэтому площадь большого квадрата составляет 16 квадратных сантиметров.
В математике мы сокращаем «квадратные сантиметры» до см 2 . 2 означает «квадрат».
Каждый квадрат сетки равен 1 см 2 .
Площадь большого квадрата 16см 2 .
Подсчет квадратов на сетке для определения площади работает для всех форм — если известны размеры сетки. Однако этот метод становится более сложным, когда фигуры не вписываются в сетку точно или когда вам нужно подсчитать доли квадратов сетки.
В этом примере квадрат не точно помещается на сетке.
Мы все еще можем вычислить площадь, считая квадраты сетки.
- Имеется 25 полных квадратов сетки (заштрихованы синим цветом).
- 10 квадратов полусетки (заштрихованы желтым цветом) — 10 полуквадратов эквивалентны 5 полным квадратам.
- Также есть 1 четверть квадрата (заштрихована зеленым) — (или 0,25 целого квадрата).
- Сложите целые квадраты и дроби вместе: 25 + 5 + 0,25 = 30,25.
Таким образом, площадь этого квадрата составляет 30,25 см 2 .
Вы также можете записать это как 30¼см 2 .
Хотя использование сетки и подсчета квадратов внутри фигуры — очень простой способ изучения концепции площади, он менее полезен для нахождения точных областей с более сложными формами, когда можно сложить много частей квадратов сетки.
Площадь можно рассчитать по простым формулам в зависимости от типа фигуры, с которой вы работаете.
Оставшаяся часть этой страницы объясняет и дает примеры того, как вычислить площадь фигуры без использования системы сеток.
Площади простых четырехугольников:
квадратов, прямоугольников и параллелограммов
Простейшие (и наиболее часто используемые) вычисления площади выполняются для квадратов и прямоугольников.
Чтобы найти площадь прямоугольника, умножьте его высоту на ширину.
Для квадрата вам нужно только найти длину одной из сторон (так как каждая сторона имеет одинаковую длину), а затем умножить это на себя, чтобы найти площадь. Это то же самое, что и длина 2 или длина в квадрате.
Рекомендуется проверять, действительно ли фигура является квадратом, измеряя две стороны. Например, стена в комнате может выглядеть как квадрат, но когда вы ее измеряете, вы обнаруживаете, что на самом деле это прямоугольник.
Часто в реальной жизни формы могут быть более сложными. Например, представьте, что вы хотите найти площадь пола, чтобы заказать нужное количество ковра.
Типовой план помещения не может состоять из простого прямоугольника или квадрата:
В этом и других подобных примерах фокус состоит в том, чтобы разделить фигуру на несколько прямоугольников (или квадратов).Неважно, как вы разделите фигуру — любое из трех решений даст один и тот же ответ.
Для решений 1 и 2 необходимо создать две фигуры и сложить их площади, чтобы найти общую площадь.
Для решения 3 вы создаете большую форму (A) и вычитаете из нее меньшую форму (B), чтобы найти площадь.
Другая распространенная проблема — найти область границы — фигуру внутри другой фигуры.
В этом примере показана дорожка вокруг поля — ширина дорожки 2 м.
Опять же, в этом примере есть несколько способов определить площадь пути.
Вы можете просмотреть путь как четыре отдельных прямоугольника, вычислить их размеры, а затем их площадь и, наконец, сложить области, чтобы получить итог.
Более быстрый способ — вычислить площадь всей формы и площадь внутреннего прямоугольника. Вычтите внутреннюю площадь прямоугольника из всей, оставив область пути.
- Площадь всей формы составляет 16 м × 10 м = 160 м 2 .
- Мы можем определить размеры средней секции, потому что знаем, что путь по краю имеет ширину 2 метра.
- Ширина всей формы составляет 16 м, а ширина пути через всю форму составляет 4 м (2 м слева от формы и 2 м справа). 16 м — 4 м = 12 м
- То же самое для высоты: 10м — 2м — 2м = 6м
- Итак, мы подсчитали, что средний прямоугольник имеет размер 12 × 6 м.
- Таким образом, площадь среднего прямоугольника составляет: 12 м × 6 м = 72 м 2 .
- Наконец, мы убираем область среднего прямоугольника из области всей формы. 160 — 72 = 88 м 2 .
Площадь тропы 88м 2 .
Параллелограмм представляет собой четырехстороннюю форму с двумя парами сторон равной длины — по определению прямоугольник является разновидностью параллелограмма. Однако большинство людей склонны думать о параллелограммах как о четырехсторонних фигурах с наклонными линиями, как показано здесь.
Площадь параллелограмма рассчитывается так же, как и для прямоугольника (высота × ширина), но важно понимать, что высота означает не длину вертикальных (или отклоненных от вертикали) сторон, а расстояние между сторонами.
Из диаграммы видно, что высота — это расстояние между верхней и нижней сторонами фигуры, а не длина стороны.
Представьте себе воображаемую линию под прямым углом между верхней и нижней сторонами. Это высота.
Области треугольников
Может быть полезно думать о треугольнике как о половине квадрата или параллелограмма.
Если вы знаете (или можете измерить) размеры треугольника, то вы можете быстро определить его площадь.
Площадь треугольника (высота × ширина) ÷ 2.
Другими словами, вы можете вычислить площадь треугольника так же, как площадь квадрата или параллелограмма, а затем просто разделите свой ответ на 2.
Высота треугольника измеряется по прямой линии от нижней линии (основания) до «вершины» (верхней точки) треугольника.
Вот несколько примеров:
Площадь трех треугольников на диаграмме выше одинакова.
Каждый треугольник имеет ширину и высоту 3 см.
Площадь рассчитана:
(высота × ширина) ÷ 2
3 × 3 = 9
9 ÷ 2 = 4,5
Площадь каждого треугольника составляет 4,5 см 2 .
В реальных ситуациях вы можете столкнуться с проблемой, которая требует от вас найти площадь треугольника, например:
Вы хотите покрасить фронтальный конец сарая. Вам нужно посетить магазин украшений только один раз, чтобы получить необходимое количество краски.Вы знаете, что литр краски покроет 10м 2 стены. Сколько краски нужно для покрытия фронтона?
Вам нужно три измерения:
A — Общая высота до вершины крыши.
B — Высота вертикальных стен.
C — Ширина здания.
В этом примере измерения:
A — 12,4 м
B — 6,6 м
C — 11,6 м
Следующий этап требует дополнительных расчетов.Представьте себе здание как две формы: прямоугольник и треугольник. По имеющимся у вас измерениям вы можете рассчитать дополнительное измерение, необходимое для определения площади фронтона.
Размер D = 12,4 — 6,6
D = 5,8 м
Теперь вы можете определить площадь двух частей стены:
Площадь прямоугольной части стены: 6,6 × 11,6 = 76,56 м 2
Площадь треугольной части стены: (5.8 × 11,6) ÷ 2 = 33,64 м 2
Сложите эти две области вместе, чтобы получить общую площадь:
76,56 + 33,64 = 110,2 м 2
Как вы знаете, один литр краски покрывает 10 м 2 стены, поэтому мы можем рассчитать, сколько литров нам нужно купить:
110,2 ÷ 10 = 11,02 л.
На самом деле вы можете обнаружить, что краска продается только в 5-литровых или 1-литровых канистрах, результат — чуть более 11 литров. У вас может возникнуть соблазн округлить до 11 литров, но, если мы не будем разбавлять краску водой, этого будет недостаточно.Таким образом, вы, вероятно, округлите до следующего целого литра и купите две 5-литровые банки и две 1-литровые банки, что в сумме даст 12 литров краски. Это позволит избежать любых потерь и оставит большую часть литра для подкраски позднее. И не забывайте, что если вам нужно нанести более одного слоя краски, вы должны умножить количество краски для одного слоя на необходимое количество слоев!
Области кругов
Чтобы вычислить площадь круга, вам необходимо знать его диаметр или радиус .
Диаметр круга — это длина прямой линии от одной стороны круга до другой, проходящей через центральную точку круга. Диаметр в два раза больше длины радиуса (диаметр = радиус × 2)
Радиус круга — это длина прямой линии от центральной точки круга до его края. Радиус составляет половину диаметра. (радиус = диаметр ÷ 2)
Вы можете измерить диаметр или радиус в любой точке окружности — важно измерять с использованием прямой линии, проходящей через (диаметр) или заканчивающейся в (радиусе) центра окружности.
На практике при измерении окружностей часто проще измерить диаметр, а затем разделить на 2, чтобы найти радиус.
Радиус нужен для вычисления площади круга, формула:
площадь круга = πR 2 .
Это означает:
π = Pi — постоянная, равная 3,142.
R = радиус окружности.
R 2 (радиус в квадрате) означает радиус × радиус.
Следовательно, круг с радиусом 5 см имеет площадь:
3.142 × 5 × 5 = 78,55 см 2 .
Круг диаметром 3 м имеет площадь:
Сначала прорабатываем радиус (3м ÷ 2 = 1,5м)
Затем примените формулу:
πR 2
3,142 × 1,5 × 1,5 = 7,0695.
Площадь круга диаметром 3 м составляет 7,0695 м 2 .
Заключительный пример
Этот пример использует большую часть содержимого этой страницы для решения простых задач с областями.
Это дом Рубена М. Бенджамина в Блумингтоне, штат Иллинойс, внесенный в Национальный реестр исторических мест США (номер записи: 376599).
Этот пример включает поиск области фасада дома, деревянной решетчатой части — исключая дверь и окна. Вам нужны следующие размеры:
| A — 9,7 м | B — 7,6 м |
| C — 8,8 м | D — 4,5 м |
| E — 2.3 мес | F — 2,7 м |
| G — 1,2 м | H — 1,0 м |
Примечания:
- Все размеры являются приблизительными.
- Не нужно беспокоиться о границе вокруг дома — она не учтена в измерениях.
- Мы предполагаем, что все прямоугольные окна имеют одинаковый размер.
- Размер круглого окна — это диаметр окна.
- Размер двери включает ступеньки.
Какова площадь деревянной реечной части дома?
Работы и ответы ниже:
Ответы на приведенный выше пример
Сначала определите площадь основной формы дома — прямоугольника и треугольника, составляющих форму.
Главный прямоугольник (B × C) 7,6 × 8,8 = 66,88 м 2 .
Высота треугольника (A — B) 9,7 — 7,6 = 2,1.
Следовательно, площадь треугольника равна (2.1 × C) ÷ 2.
2,1 × 8,8 = 18,48. 18,48 ÷ 2 = 9,24 м 2 .
Общая площадь фасада дома равна сумме площадей прямоугольника и треугольника:
66,88 + 9,24 = 76,12 м 2 .
Затем проработайте площади окон и дверей, чтобы их можно было вычесть из всей площади.
Площадь двери и ступенек составляет (D × E) 4,5 × 2,3 = 10,35 м 2 .
Площадь одного прямоугольного окна составляет (G × F) 1.2 × 2,7 = 3,24 м 2 .
Есть пять прямоугольных окон. Умножьте площадь одного окна на 5.
3,24 × 5 = 16,2 м2. (общая площадь прямоугольных окон).
Круглое окно имеет диаметр 1 м и радиус 0,5 м.
Используя πR 2 , определите площадь круглого окна: 3,142 × 0,5 × 0,5 =. 0,7855 м 2 .
Затем сложите площади двери и окон.
(зона двери) 10,35 + (прямоугольная зона окон) 16.2 + (площадь круглого окна) 0,7855 = 27,3355
Наконец, вычтите общую площадь окон и дверей из всей площади.
76,12 — 27,3355 = 48,7845
Площадь деревянного реечного фасада дома и ответ на проблему: 48,7845м 2 .
Вы можете округлить ответ до 48,8 м 2 или 49 м 2 .
См. Нашу страницу на Оценка, приближение и округление .
фактов о кругах для детей — площадь, радиус, диаметр, окружность, дуга, касательная, хорда, сектор, сегмент
Круг — это круглая двумерная форма, которая похожа на букву «О».
На строгом математическом языке круг относится к границе формы, в то время как «диск» используется для обозначения всей формы, включая внутреннюю часть.
Прямая линия от центра круга до края называется радиусом.
Прямая линия, проходящая от одной стороны окружности к другой через центр, называется диаметром.
Расстояние по внешней стороне круга называется окружностью.
Все точки на краю круга находятся на одинаковом расстоянии от центра.
Значение Пи (π) с точностью до 2 знаков после запятой равно 3,14, оно пригодится при вычислении длины окружности и площади круга.
Окружность круга определяется по следующей формуле: Окружность = π d
Площадь круга можно найти по следующей формуле: Площадь = π r²
Дуга — это часть окружности.
Хорда — это прямая линия, соединяющая две точки на окружности, диаметр — это пример хорды (самой длинной из возможных).
Сегмент — это область между хордой и дугой, которую он соединяет.
Касательная — это прямая линия, которая касается одной точки окружности.
Сектор — это область между дугой и двумя радиусами.
Полная дуга окружности составляет 360 градусов.
Полукруг — это форма, которая образует полукруг, дуга полукруга имеет размер 180 градусов.
Круги обладают высокой симметрией.
У круга самый короткий периметр из всех форм с одинаковой площадью.
Форма круга любима людьми, и ее можно увидеть во многих рисунках.
Изобретение колеса (в форме круга) было одним из самых важных в истории человечества.
Круги и сферы также часто встречаются в природе. Можете ли вы привести примеры?