Расчет объема трубы: Калькулятор объема трубы онлайн
Калькулятор объема трубы онлайн
Для расчета объема трубы введите в калькулятор внутренний диаметр (в миллиметрах) и длину трубы (в метрах). В результате вы увидите полный объем и объем погонного метра, как в метрах кубических, так и в литрах.
Объем трубы важен при расчете систем отопления, газопроводов и водопроводов. Так же при строительстве скважин и колодцев.
Поделитесь с друзьями в соцсетях…Похожие калькуляторы:
Раздел: Строительные калькуляторыОбъем трубы. Расчета внешнего и внутреннего объема для труб различного профиля
Объем воды в трубе, как и некоторые другие параметры, приходится просчитывать при прокладке коммуникаций и выполнении ремонтных работ. Неаккуратное проведение расчетов может обернуться неприятностями в виде излишних затрат на транспортировку и монтаж. Куда худшими последствиями небрежности станут недостаточное или избыточное давление в системе, что приведет к неизбежным переделкам из-за низкой производительности или преждевременного износа.
От такого параметра, как объем трубы, зависит количество рабочей среды, которая будет транспортироваться по трубопроводу
Как выполняется расчет на промышленном объекте
Объем водопроводной, газовой, канализационной или отопительной трубы рассчитывается в двух видах:
- Внешнем или фактическом.
- Внутреннем или полезном.
Перед тем, как посчитать объем трубы, следует определиться, о каком именно виде идет речь. Если требуется рассчитать объемы газа или жидкости, которые будут перекачиваться, то расчет относится к внутреннему или полезному виду.
На значительных по масштабам объектах начало работ сопряжено с проведением входного контроля, ставящего целью проверку труб на предмет наличия:
- сопроводительной документации;
- сертификатов;
- маркировки, нанесенной компанией-производителем на поверхности изделий.
На этом этапе получают все необходимые сведения о трубопрокате, включая номинальные размеры, что позволяет проведение требуемых вычислений. Для того, чтобы выполнить расчет объема наиболее распространенной трубы с круглым сечением, нужно получить данные о ее длине и диаметре.
Полезно знать! Фактическую длину на производственном объекте замеряют, используя строительную рулетку или мерную проволоку. При этом отмечается имеющиеся отклонения от данных, внесенных в заводскую документацию, и их соответствие нормативам, установленным ГОСТами.
Сверку наружного диаметра проводят, пользуясь формулой:
D = L : π — 2∆p – 0,2 мм.
Здесь задействованы такие величины: D – наружного диаметра; L – длины внешней окружности изделия; π — 3,14; ∆p – толщины материала, использованного для изготовления строительной рулетки; допустимого припуска в 0,2 мм, относящегося к прилеганию мерного инструмента к поверхности изделия.
При проведении сверки наружного диаметра учитываются установленные ГОСТами значения отклонений и погрешностей.
Как выполняется расчет внешнего (фактического) объема круглой трубы
Основной величиной, необходимой при проведении вычислений, будет диаметр изделия. Следует учитывать, что измерения стальных труб традиционно принято выполнять в так называемой имперской системе, оперирующей дюймами и долями дюймов. Переводя в более привычную метрическую систему, принимаем величину дюйма за 25, 4 мм. Однако для диаметра трубы в обычном исполнении он принимается за 25,5 мм, в усиленном исполнении – за 27,1 мм. Незначительными отклонениями принято пренебрегать, применяя в выполнении расчетов безразмерную величину условного прохода – Ду, определяемого с использованием специальных таблиц.
Выполнение соединений стальных труб с диаметром, указанным в имперской системе – в дюймах, с пластиковыми, алюминиевыми или медными, диаметр которых принято указывать, используя метрическую систему, в миллиметрах, проводится при помощи специальных переходников.
Расчет объема воды для системы теплоснабжения сводится, по обыкновению, к определению необходимости в незамерзающей жидкости, чтобы избежать расходов при появлении излишков. Вычисления сводятся к использованию размеров расширительного бака, замеру его диаметров:
- внешнего;
- внутренней полости.
Измеряя диаметр трубы в метрической системе, следует знать, как правильно перевести полученное значение в дюймы
Используется формула объема цилиндра:
V = πR2H.
Здесь мы имеем дело с V – искомым внешним (фактическим объемом) круглой трубы; π – 3,14; R – внешним радиусом изделия; H – высотой цилиндра или длиной трубы.
Выполнение расчета внутреннего (полезного) объема круглой трубы
Такой показатель, как толщина стенок, оказывает довольно значительное влияние на определение объема труб, определяя разницу между внешним и внутренним (полезным и фактическим).
Обратите внимание! Так как при поставках стальных водогазопроводных изделий принято оперировать лишь величиной условного прохода Ду и типом (легким, обыкновенным или усиленным), то для вычисления объема приходится обращаться к табличным данным, содержащимся в ГОСТе 3262-75.
Работа с ГОСТовской таблицей ведется в таком порядке:
- Из левой колонки берется величина условного прохода — Ду и соответствующее ей значение наружного диаметра в следующей колонке.
- Зная тип трубы, производится вычитание из величины наружного диаметра удвоенной толщины стенки.
- Полученное значение внутреннего диаметра делением на два превращается в значение радиуса внутреннего сечения.
Для вычисления площади данного сечения пользуются формулой
S = πr2, где:
S – искомая площадь; π – 3,14; r – радиус внутреннего сечения.
Определение внутреннего (полезного) объема круглой трубы осуществляется посредством формулы
V = SL, в которой:
V – искомый внутренний (полезный) объем; S – площадь внутреннего сечения; L – длина трубы.
Для расчета полезного объема трубы нужно знать ее внутренний диаметр
Проведем вычисление полезного объема обыкновенной трубы при условном проходе, равном 100. Табличное значение наружного диаметра в этом случае будет равняться 114 мм, а толщины стенок – 4,5 мм. Произведя вычитание 114 – 2х4,5, получим значение внутреннего диаметра – 105 мм, половину которого составит радиус, равный, соответственно, 52,5 мм. Переведем для удобства дальнейших расчетов в метры – 0,0525 м. Площадь сечения составит 0,0525 м, умноженные на π -0,16485 м3, округляемые до 0,165 м3. Для перевода в литры полученное значение умножается на 1000, получаем – 165 литров.
Как выполняются расчеты объема труб с профильным сечением
Как правило, описывая проведение вычислений объема трубопроката, по умолчанию ведут речь исключительно об изделиях круглого сечения. Однако в современный обиход все более активно включаются профильные трубы, обладающие различным по форме сечением:
- овальным;
- квадратным;
- прямоугольным;
- трапециевидным.
При прямоугольном сечении вычисление объема трубы ведется по формуле V = SH (в развернутом виде – abH), т. е. требуются данные о габаритах изделия – длине, ширине, высоте. При сечении 15х10 мм для пятиметрового отрезка получаем 0,015х0,010х5, что равняется 0,0075 м3 или семи с половиной литрам.
Вычисления для изделия с квадратным сечением упрощаются, так как необходимо знать значения только одной стороны сечения и длины. Формула такова:
V = а2H.
При сечении 180х180 мм для пятиметрового отрезка получаем 0,182х5, что равняется 0,16 м3 или 160 литрам.
При овальном сечении применяют формулу:
V = SL.
Вычисление площади овального сечения ведется с использованием формулы S = πав, где нужно подставить значения длины большой и малой полуосей эллипса (овала).
Проще всего рассчитать объем квадратной профильной трубы, так как все четыре ее стороны одинаковые
Трапециевидное сечение труб, все чаще используемое, наряду с прямоугольным, при обустройстве канализации или дымохода, для определения объема предполагает применение все той же формулы V = SL. Для вычисления площади трапеции берется формула S = 0,5 ав.
Появление все большего количества специальных компьютерных программ для проведения расчетов в отношении трубопроката различного профиля позволяет существенно упростить процесс. Достаточно воспользоваться услугами какого-либо онлайн-калькулятора и ввести имеющиеся в распоряжении данные, чтобы моментально получить необходимые результаты.
Расчитать объем воды в трубе
На чтение 9 мин. Обновлено
Трубы настолько широко применяется в народном хозяйстве, что перечислить все направления их использования просто невозможно. И очень часто нужно определить объем трубы, для чего применяется онлайн калькулятор. Используя этот инструмент можно быстро и достаточно точно высчитать объем единичного изделия или цельного трубопровода любой протяжённости.Предлагаем вам воспользоваться нашим бесплатным онлайн калькулятором для определения объема воды в трубе.
При расчете Вы узнаете объем воды или любой другой жидкости в одном метре трубы, так же сможете рассчитать объем во всем трубопроводе и площадь поверхности рассчитываемого участка.
Введите параметры для расчёта в онлайн калькулятор
Предлагаем ввести параметры в для расчета объёма в онлайн калькулятор.

Почему необходимо заранее рассчитать объем жидкости в трубе калькулятором, только после этого приступать к закупкам? Ответ очевиден – для того чтобы определить, сколько надо приобрести теплоносителя, чтобы заполнить систему отопления дома. Особенно это важно для домов периодического посещения, которые на длительное время остаются холодными. Вода внутри такой отопительной системы неминуемо замерзнет, разрывая проводящие элементы и радиаторы. Кроме того, нужно учитывать и моменты которые перечислены в расположенном ниже списке.
- Вместимость расширительного бачка. Этот параметр всегда указывается в паспорте на это изделие, но если такая возможность отсутствует, можно просто заполнить емкость определенным количеством литров воды, после чего использовать эту информацию.
- Емкость нагревательных элементов – радиаторов отопления. Такие данные также можно получить из технического паспорта или инструкции для одной секции. После чего, воспользовавшись проектными данными, умножить емкость одной секции на их общее число.
- Количество жидкости внутри различных узлов, а также системах управления и контроля, например – тепловых насосов, манометрах и тому подобное. Впрочем, эта величина будет небольшой, не выше статистической погрешности, поэтому данные третьего пункта обычно игнорируют.
Если система водоснабжения или отопления выполняется из металлических изделий, нужно учитывать некоторые их особенности. Так, водогазопроводный сортамент по ГОСТ 3262-84 выпускается трех серий:
- легкая;
- средняя;
- тяжелая.
При этом различие состоит именно по толщине стенок, что при равенстве внешнего размера, говорит об уменьшении внутреннего сечения для разных исполнений. Поэтому при закупке следует обращать внимание именно на этот показатель, чтобы внутренний проход был одинаков по всей протяженности водопровода или отопления. Расчет объема жидкости в трубе, с использованием калькулятора можно произвести, воспользовавшись следующей формулой:

- V – объем метра трубы, см3.
- 100 – длина, см.
- Число «пи», равное 3.14.
- Радиус внутреннего канала, см. здесь – площадь поперечного сечения внутренней полости.
При расчете нужно руководствоваться не сертификатными данными или вывеской продавца. Желательно тщательно измерить размер внутреннего отверстия, используя штангенциркуль, а при подсчете руководствоваться именно этими данными.
Если конструкция этого измерительного прибора не позволяет производить внутренние замеры, можно мерить наружный диаметр и толщину стенки. Затем первого замера нужно вычесть удвоенный второй, после чего получить достоверный размер проходного отверстия.
Кроме принадлежности к одной серии, о чем упоминалось выше, нужно учитывать возможность использования исходного материала на минусовых допусках, что закономерно повлияет на размер сечения в сторону его увеличения. Если есть возможность воспользоваться при закупке интернетом, можно использовать встроенный программный calculator, рассчитать объем воды в трубе онлайн. Но при этом исходные данные нужно водить реальные. Настоятельно рекомендуем перед использованием калькулятора ознакомиться с инструкцией, в таком случае расчеты будут верными со стопроцентной гарантией.
С их использованием должны рассчитываться также другие параметры системы, включая вес погонного метра и прочее. Широкое применение при выполнении таких операций нашли специально разработанные таблицы. Но они справедливы только для номинальных размеров, любые отклонения они не учитывают. Определяя объем воды в трубе онлайн калькулятором, ошибиться маловероятно.
Как произвести расчет без калькулятора
Трубопроводный транспорт в условиях России играет очень важную роль. По нему перекачиваются огромные количества жидких продуктов. Кроме воды транспортируется сжиженный газ, нефть и продукты её переработки и другие жидкости, в ряде случаев агрессивные.
Алгоритм расчёта вместимости трубы несложен – нужно узнать площадь поперечного сечения и умножить её на длину изделия. Она определяется условиями её транспортировки по железной дороге, база вагона равняется 11,7 метра, поэтому они производятся длиной 11,3-11,7 м.
Вместимость такого изделия определяется диаметром внутреннего пространства, например для размера 820 х 10 миллиметров рабочий диаметр мы можем определить соотношением Д = 820 – 10 х 2 = 800 мм. Однако, лучше сразу перейти к общепринятой единице – метру. При внутреннем диаметре изделия 0,8 метра соотношение для расчёта выглядит следующим образом:
V = П*r2l
где:- V – объем;
- П – число пи, равное 3,14;
- r – радиус;
- l – её длина.
Однако высчитывать объем одиночного изделия не имеет смысла. Лучше сразу применить это соотношение для определения объёма всего трубопровода.
Этот показатель важен для того чтобы знать количества перекачиваемого продукта, которое останется в трубопроводе по окончании транспортировки нужного объема. Однако трубопроводы не используются в режиме разовой перекачки. Они предназначены для постоянной эксплуатации.
По такой же методике рассчитываются объёмы емкостей цилиндрической формы – цистерн, бочек и прочих подобных.
В трубопроводном транспорте для магистралей используются в основной массе электро сварные одно или двух шовные трубы с различной толщиной стенок. Для повышения производительности трубопровода продукты по нему перекачиваются под большим давлением – до 130 атмосфер.
Поэтому для производства используется листовой металл толщиной до 36 миллиметров. Основной способ соединения в трубопроводах – электросварка, поэтому в качестве материала изготовления используются стали с низким содержанием углерода, такие, как 09Г2С, 09Г2ФБ и другие подобные.
Основным регламентирующим документом для производства электро сварных прямо шовных труб являются ГОСТы 10804 и 10805, однако применяются также множество технических параметров, предусматривающих определенные условия изготовления труб которые будут эксплуатироваться в агрессивной среде.
Важным направлением применения труб являются вентиляционные системы промышленного и бытового назначения. Для обеспечения прочностных показателей в них чаще всего используются прямоугольные короба, рассчитывать вместимость которых гораздо проще.
Коробчатые трубопроводы для вентиляции производятся, как правило, из оцинкованной стали, имеющей длительный срок эксплуатации. Но в последнее время наметилась тенденция применение для вентиляционных систем из пластиковых материалов, срок службы которых может превышать этот показатель для металлических аналогов.
Это же относится к использованию пластиков для водопроводных напорных и самотёчных систем.
Точное определение объёма труб и трубопроводов из них доступно всем пользователям сети Интернет и это позволяет избежать серьёзных ошибок при проектировании самых различных объектов народного хозяйства.
Расчёт объёма трубы
Для расчёта объёма трубы нужно воспользоваться школьными знаниями по геометрии. Есть несколько способов: 1. Умножив площадь поперечного сечения фигуры на её длину в метрах, полученный результат будет метры в кубе. 2. Возможно, узнать величину водопровода и в литрах. Для этого объём умножается на 1000 — это количество литров воды в 1 кубометре. 3. Третий вариант — сразу считать в литрах. Понадобится измерения делать в дециметрах — длину и площадь фигуры. Этот более сложный и неудобный способ.
Чтобы вычислить в ручную – без калькулятора, потребуется штангенциркуль, линейка и калькулятор. Для облегчения процесса по определению размера объёма трубы можно воспользоваться онлайн-калькулятором.
Формула для расчёта объёма трубы
Процесс расчёта объёма системы отопления выглядит следующим образом.
Определим площадь сечения трубы
Чтобы узнать точное значение, необходимо сначала рассчитать площадь поперечного сечения. Для этого, следует воспользоваться формулой:
S = R2 х Пи
Где R является радиусом трубы, а число Пи равно 3,14. Так как ёмкости для жидкости,как правило, имеют круглую форму, то R возводится в квадрат.
Рассмотрим, как можно сделать вычисления, имея диаметр изделия 90 мм:
- Определяем радиус — 90 / 2 = 45 мм, в пересчёте на сантиметры 4,5.
- Возводим 4,5 в квадрат, получается 2,025 см2.
- Подставляем данные в формулу — S = 2 х 20,25 = 40, 5 см2.
Если изделие профилированное, то нужно считать по формуле прямоугольника — S = а х b, где а и b — размер сторон (длина). При определении размера сечения профиля с длиной сторон 40 и 50, необходимо 40 мм х 50 мм = 2000 мм2 или 20 см2.

Для вычисления сечения, необходимо знать внутренний диаметр трубы, который измеряется штангенциркулем, но это не всегда возможно. Если известен только наружный диаметр, и не знаем толщину стен, то потребуются более сложные вычисления. Стандартная толщина бывает 1 или 2 мм, у изделий большого диаметра может достигать 5 мм.
Важно! Приступать к расчёту лучше при наличии точных показателей о толщине стен и внутреннем радиусе.
Формула расчёта объёма трубы
Рассчитать объём трубы в м3, можно воспользовавшись формулой:
V = S х L
То есть, требуется знать всего два значения: площадь сечения (которая была определена заранее) (S) и длина (L).
К примеру, длина трубопровода 2 метра, а площадь сечения пол метра. Для вычисления необходимо взять формулу, по которой определяется площадь круга, и вставить внешний размер поперечины металла:
S = 3,14 х (0,5 / 2) = 0,0625 кв.м.
Итоговый результат будет следующим:
V = HS = 2 х 0,0625 = 0,125 метра куб.
H — толщина стенки
Производя расчёт, важно чтобы во всех показателях была одна единица измерения, иначе результат получится неправильным. Проще брать данные в см2.
Объём водопровода в литрах
Легко посчитать объём жидкости в трубе без калькулятора, если знать внутренний её диаметр, но это не всегда можно сделать, когда радиаторы или отопительные котлы для воды имеют сложную форму. Сегодня такие изделия не редко применяются в строительной сфере, при обустройстве тёплых полов. Поэтому, следует изначально выяснить параметры конструкции, эту информацию можно найти в техпаспорте или сопроводительной документации. Чтобы посчитать размер не стандартной емкости, необходимо залить в неё воду, которая заранее измерена.
Кроме того, кубатура воды будут зависеть и от материала, из которого изготовлен водопровод. К примеру, изделие из стали пропустит на порядок меньше воды, чем равное по размеру полипропиленовое или пластиковое. На это влияет поверхность изнутри, железная более шероховатая, что сказывается на проходимости.
Поэтому, необходимо делать вычисления на каждую ёмкость, если она изготовлена из другого материала, и затем сложить все показатели. Можно воспользоваться специальными сервис-программами или калькуляторами, сегодня их много в интернете, они существенно облегчат процесс установления количества воды в системе.
площадь трубы для воды, формула в м³, калькулятор онлайн, сечение и поверхность
 При монтаже труб важно знать их объем
При монтаже труб важно знать их объемРасчет объема необходим для определения вместимости какой-либо емкости, также отражает размеры определенного объекта. Для упрощения всех расчетов, можно использовать онлайн-калькулятор, но не всегда есть возможность им пользоваться. Проще сделать несколько замеров, и умножить между собой получившиеся цифры.
Измерения для расчета объема труб
Некоторые для этого пользуются онлайн-калькуляторами, а другие, пользуясь формулами, рассчитывают объем трубы вручную. Есть и другие, несколько иные, способы расчета объема труб, например, с использованием таблиц. В строительстве, причем не только в промышленных масштабах, но и в домашних условиях, иногда рассчитывается объем.

Так, иногда возникает необходимость расчета объема труб, например, при обустройстве:
- Водопровода;
- Канализации;
- И иных нужд, где используются трубы.
Для правильного определения объема какой-либо трубы в м3, например, ВГП трубы, следует проделать определенные манипуляции. Измерить внутренний радиус трубы, или же определить внутренний, а также внешний диаметр трубы и записать полученные результаты. Измерить длину трубы, и также записать полученные значения. Для расчета, какой объем воды может вместить труба, необходимо перевести миллиметры в метры, далее необходимо радиус возвести в квадрат и умножить его на число Пи, таким образом, будет определено сечение.
Пи равно значению 3,14.
Далее длину трубы следует умножить на площадь ее сечения, таким достаточно нехитрым способом можно найти объем. Таблица представляет собой несколько столбцов, в которых прописаны внутренний и внешний диаметр труб, указана погонная длина (как правило, это 10 м) и объем 1 м в литрах. Достаточно найти в таблице подходящую по размеру трубу для того, чтобы определить ее объем.
Расчет площади труб
Помимо определения объема труб, требуется иногда рассчитать и площадь, например, для того, чтобы знать, сколько потребуется краски для окрашивания или покрытия каким-либо иным материалом. Расчет площади также производиться либо с помощью онлайн калькуляторов, либо с использованием формулы.

Таким образом, можно заранее вычислить, какой объем материала потребуется для:
- Покраски;
- Покрытия изоляцией;
- Обезжиривания поверхности трубы.
Формула для расчета площади используется не сложная. Сначала требуется измерить длину трубы, а также определить ее внешний радиус, все полученные сантиметры (если труба небольшого размера) переводятся в метры. Пи, равное 3,14, нужно умножить на 2, далее получившееся число умножается на длину и радиус трубы.
В результате всех расчетов можно узнать, чему равна площадь трубы.
Для определения площади квадратной трубы, нужно сначала вычислить ее периметр, а уже получившееся число умножить на длину. Тоже самое касается и трубы в форме прямоугольника – расчет производится точно также. Но, так считать просто, если трубы имеют прямую форму, а если они изогнутые, то необходимо к полученным цифрам добавлять определенные допуски. Такую информацию можно отыскать в специальных строительных нормах.
Подробный расчет площади трубы
Для самых разных целей требуется знать, какая площадь будет у какой-либо трубы. Посчитать ее можно с помощью онлайн-калькулятора или же с помощью простых формул. Для расчета площади трубы, например, стальной, необходимо воспользоваться алгоритмом.

Алгоритм:
- Сначала следует определить диаметр трубы, полученный результат необходимо умножить на число Пи.
- Полученную цифру следует умножить на длину трубы, в результате чего будет известна внешняя площадь.
- Если требуется высчитать внутреннюю площадь трубы, формула несколько изменяется, сначала также определяется диаметр, после измеряется толщина ее стенок.
- Из диаметра вычитают толщину стенок трубы, и полученный результат снова умножается на длину.
Расчет наружной площади необходим для того, чтобы знать, какое количество краски или укрывного материала понадобится для трубы. Также это знание поможет при проектировании систем теплоснабжения с тем, чтобы знать, какие теплопотери могут быть.
Расчет внутренней площади необходим для определения объема кубатуры жидкости, которая может проходить через трубу.
Помимо расчета площади труб, предназначенных для жидкости, есть воздуховодные варианты, для круглой расчет примерно такой же. А вот для расчета площади овала или овальной трубы, следует определить 2 радиуса, после чего их следует перемножить между собой, и получившийся результат умножить на число Пи.
Вычисление площади сечения трубы
Большинство вычислений для разных нужд в современном мире производится с помощью онлайн-расчетов. Зная необходимые параметры, их следует подставить в соответствующие поля с тем, чтобы узнать результат. Но не всегда есть возможность воспользоваться такими «помощниками». В этом случае считать, например, площадь сечения трубы, приходится вручную.

Расчет:
- Труба чаще всего имеет форму круга и реже встречается в форме квадрата или овала.
- Для расчета круглой трубы, необходимо определить ее диаметр, поучившееся значение следует умножить на число Пи.
- Для определения внутреннего сечения трубы, из получившегося числа следует прибавить к стенке, для удобства все расчеты лучше всего производить в метрах.
Расчет площади сечения необходим для того, чтобы знать скорость движения жидкости или газов, и для этого необходимо выбрать наиболее оптимальный диаметр круглого трубопровода. Также при расчете следует учитывать температуру газа или жидкости, с которой они двигаются по трубам.
Для более качественного расчета площади сечения какой-либо металлической трубы, следует пользоваться дополнительно специальными строительными таблицами и справочниками.
Но, если производится расчет сечения самотечных трубопроводов, следует принимать во внимание не полное сечение трубы, а так называемое живое или фактическое. Сечение живого потока обычно равно половине фактического сечения трубы.
Математическая формула расчета объема
Для расчета объема какой-либо трубы, следует воспользоваться формулой расчета объема цилиндра, так как труба по сути своей представляет цилиндр.

Алгоритм расчета:
- Сначала следует определить размер поперечного сечения трубы;
- Из полученной цифры следует вычесть толщину стенок трубы;
- Полученную цифру разделить на 2, чтобы определить радиус трубы.
Если нет возможности определить радиус, то в этом случае следует ориентироваться на размер окружности трубы, получившийся результат следует разделить на число Пи в квадрате (примерно 9,85). Следует также определить площадь сечения, для этого снова следует воспользоваться числом Пи, которое умножают на квадрат радиуса. Причем квадрат радиуса может быть рассчитан, как в метрах, так и сантиметрах, все зависит от диаметра самой трубы.
Для определения объема воды или иной жидкости, в выше приведенные расчеты следует подставить размеры внутреннего диаметра трубы.
Если нет большого желания что-либо рассчитывать по формуле, можно воспользоваться специальными таблицами для расчета погонного метра какой-либо трубы в литрах. В таких таблицах указано, сколько воды или иной жидкости может через себя пропустить погонный метр в литрах или же кубах. Расчет такого параметра важен при проектировании систем отопления. Также следует учитывать такую особенность – трубы, изготовленные из стали, пропускают объема воды меньше из-за шероховатостей и отложений внутри, чем, например, пропиленовые, при расчете следует это учитывать.
Определение площади поверхности трубы
Важно определять площадь поверхности, так как это позволяет рассчитать, какое количество грунта, краски или укрывного материала потребуется для той или иной трубы с учетом ее формы, материала и веса. Масса труб, изготовленных из ПВХ или пропилена, значительно меньше, чем стальных, хотя площадь их одинакова.

Для вычисления площади трубы, потребуется выполнить следующие действия:
- Определить радиус трубы сначала в сантиметрах;
- После перевести полученный результат в метры;
- После следует высчитать длину трубы также в метрах;
- Умножить полученный результат на известный радиус, в результате чего можно узнать внешнюю площадь трубы.
Можно вычислить площадь и прямоугольной трубы с учетом веса, достаточно знать, сколько весит погонный метр, тоннаж можно определить по специальным таблицам, применяемым в строительстве. Данную величину следует умножить на длину трубы в метрах. Такие расчеты позволяют определить количество краски, грунта и теплоизоляционного материала, а также потери тепла при передаче последнего от такого теплового узла, как котельная.
Определение внутренней площади трубы необходимо и для расчета ее максимальной проходимости.
Водопроводные трубы: как рассчитать объем (видео)
Практически каждому человеку доступны расчеты, достаточно знать все необходимые параметры, квадратуру, овальность и плотность потока жидкости в трубе. Если возникают трудности при расчете, то лучше всего обратиться к специалистам. Благодаря данной информации, каждый человек, используя необходимые данные, может вычислить необходимые параметры, в том числе по длине, площадь.
Оцените статью: Поделитесь с друзьями!  И Н С Т Р У К Т И О Н С Этот калькулятор ultra отличается тем, что позволяет выбирать между большое разнообразие единиц (6 для диаметра и 24 каждого для скорости и расхода). В отличие от других калькуляторов, вы НЕ ограничен вводом диаметра в дюймах, скорости в милях в час и т. д., что делает этот калькулятор довольно универсален. 1) Вода течет со скоростью 36 дюймов в секунду и со скоростью
1.0472 кубических фута в секунду. Какой диаметр трубы? 3) Вода течет по трубе диаметром 2 фута со скоростью 20 дюймов в секунду. Какая скорость потока? Для удобства чтения числа отображаются в формате «значащих цифр», поэтому вы , а не , см. Такие ответы, как 77.3333333333333333. Числа больше более 1000 будет отображаться в экспоненциальном представлении и с таким же количеством указаны значащие цифры.Вы можете изменить значащие цифры, отображаемые изменение числа в поле выше. Internet Explorer и большинство других браузеров будут отображать ответы правильно, но есть несколько браузеров, которые вообще не выводят без вывода . Если да, введите ноль в поле выше. Это устраняет все форматирование, но лучше, чем не видеть вывод вообще. |
Калькулятор объема
Ниже приводится список калькуляторов объема для нескольких распространенных форм. Заполните соответствующие поля и нажмите кнопку «Рассчитать».
Калькулятор объема сферы
 |
Калькулятор объема конуса
 |
Калькулятор объема куба
 |
Калькулятор объема цилиндра
 |
Калькулятор объема прямоугольного резервуара
 |
Калькулятор объема капсулы
 |
Калькулятор объема сферической крышки
Для расчета укажите любые два значения ниже.
 |
Калькулятор объема конической ствола
 |
Калькулятор объема эллипсоида
 |
Калькулятор объема квадратной пирамиды
 |
Калькулятор объема трубки
 |
Калькулятор площади сопутствующих поверхностей | Калькулятор площади
Объем — это количественная оценка трехмерного пространства, которое занимает вещество.Единицей измерения объема в системе СИ является кубический метр, или м 3 . Обычно объем контейнера определяется его вместимостью и тем, сколько жидкости он может вместить, а не объемом пространства, которое фактически вытесняет контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы могут быть разбиты на более простые совокупные формы, а сумма их объемов используется для определения общего объема. Объемы других, еще более сложных фигур можно рассчитать с помощью интегрального исчисления, если существует формула для границы фигуры.Помимо этого, формы, которые нельзя описать известными уравнениями, можно оценить с помощью математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Сфера
Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, которые равноудалены от данной точки в ее центре, где расстояние между центром и любой точкой на сфере составляет радиус r .Вероятно, самый известный сферический объект — это идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и расчет их объемов одинаков. Как и в случае с кругом, самый длинный отрезок, который соединяет две точки сферы через ее центр, называется диаметром d . Уравнение для расчета объема шара приведено ниже:
EX: Клэр хочет заполнить идеально сферический воздушный шар с радиусом 0.15 футов с уксусом для борьбы с ее заклятым врагом Хильдой на воздушных шарах в ближайшие выходные. Необходимый объем уксуса можно рассчитать с помощью приведенного ниже уравнения:
объем = 4/3 × π × 0,15 3 = 0,141 фута 3
Конус
Конус — это трехмерная форма, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус образован аналогично окружности набором отрезков прямых, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую окружность (или другую основу).На этой странице рассматривается только случай конечного правого кругового конуса. Конусы, состоящие из полукруглых линий, некруглых оснований и т. Д., Которые простираются бесконечно, не рассматриваются. Уравнение для расчета объема конуса выглядит следующим образом:
, где r — радиус, а h — высота конуса
EX: Би полна решимости выйти из магазина мороженого, потратив свои с трудом заработанные 5 долларов. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, несомненно, больше.Она определяет, что на 15% предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15% больше, чем вафельный рожок. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью следующего уравнения:
объем = 1/3 × π × 1,5 2 × 5 = 11,781 дюйм 3
Беа также вычисляет объем сахарного рожка и обнаруживает, что разница составляет <15%, и решает купить сахарный рожок.Теперь все, что ей нужно сделать, это использовать свой ангельский детский призыв, чтобы заставить посох выливать мороженое в ее рожок.
Куб
Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых пересекаются в каждой из его вершин, и все они перпендикулярны своим соответствующим смежным граням. Куб — частный случай многих классификаций геометрических фигур, включая квадратный параллелепипед, равносторонний кубоид и правый ромбоэдр.Ниже приведено уравнение для расчета объема куба:
объем = 3
где a — длина ребра куба
EX: Боб, который родился в Вайоминге (и никогда не покидал штат), недавно посетил свою исконную родину, Небраску. Пораженный великолепием Небраски и окружающей средой, непохожей на какие-либо другие, с которыми он когда-либо сталкивался, Боб знал, что должен привезти с собой домой часть Небраски. У Боба есть чемодан кубической формы с длиной по краям 2 фута, и он рассчитывает объем почвы, который он может унести с собой домой, следующим образом:
объем = 2 3 = 8 футов 3
Цилиндр
Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от данной прямой оси.Однако в обычном использовании «цилиндр» относится к правильному круговому цилиндру, где основания цилиндра представляют собой окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой h и радиусом r . Уравнение для расчета объема цилиндра показано ниже:
объем = πr 2 ч
где r — радиус, а h — высота резервуара
EX: Кэлум хочет построить замок из песка в гостиной своего дома.Поскольку он является твердым сторонником рециркуляции, он извлек три цилиндрических бочки с незаконной свалки и очистил бочки от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который может вместить каждая, используя следующее уравнение:
объем = π × 3 2 × 4 = 113.097 футов 3
Он успешно строит замок из песка в своем доме и в качестве дополнительного бонуса экономит электроэнергию на ночном освещении, так как его замок из песка светится ярко-зеленым в темноте.
Прямоугольный бак
Прямоугольный резервуар — это обобщенная форма куба, стороны которого могут иметь разную длину. Он ограничен шестью гранями, три из которых пересекаются в его вершинах, и все они перпендикулярны своим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
объем = длина × ширина × высота
EX: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к торту.Она планирует отправиться в поход по тропе Калалау на Кауаи, и, хотя она в очень хорошей форме, Дарби беспокоится о своей способности пройти тропу из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет набить свою идеально прямоугольную упаковку длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может поместить в свою упаковку, рассчитан ниже:
объем = 2 × 3 × 4 = 24 фута 3
Капсула
Капсула — это трехмерная геометрическая форма, состоящая из цилиндра и двух полусферических концов, где полусфера — это полусфера.Отсюда следует, что объем капсулы можно рассчитать, объединив уравнения объема для сферы и правого кругового цилиндра:
| объем = πr 2 ч + | πr 3 = πr 2 ( | р + з) |
, где r — радиус, а h — высота цилиндрической части
EX: Имея капсулу радиусом 1,5 фута и высотой 3 фута, определите объем растопленного молочного шоколада, который Джо может унести в капсуле времени, которую он хочет похоронить для будущих поколений на пути к самопознанию. Гималаи:
объем = π × 1.5 2 × 3 + 4/3 × π × 1,5 3 = 35,343 фута 3
Сферический колпачок
Сферический колпачок — это часть сферы, которая отделена от остальной сферы плоскостью. Если плоскость проходит через центр сферы, сферическая крышка называется полусферой. Существуют и другие различия, включая сферический сегмент, где сфера сегментируется двумя параллельными плоскостями и двумя разными радиусами, где плоскости проходят через сферу. Уравнение для вычисления объема сферической крышки выводится из уравнения для сферического сегмента, где второй радиус равен 0.Относительно сферической крышки, указанной в калькуляторе:
Имея два значения, калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:
Для r и R : h = R ± √R 2 — r 2
где r, — радиус основания, R — радиус сферы, а h — высота сферической крышки.
EX: Джек действительно хочет победить своего друга Джеймса в игре в гольф, чтобы произвести впечатление на Джилл, и вместо того, чтобы тренироваться, решает саботировать мяч для гольфа Джеймса.Он отрезает идеальную сферическую крышку от верхней части мяча для гольфа Джеймса и должен рассчитать объем материала, необходимый для замены сферической крышки и перекоса веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:
объем = 1/3 × π × 0,3 2 (3 × 1,68 — 0,3) = 0,447 дюйма 3
К несчастью для Джека, за день до игры Джеймс получил новую партию мячей, и все усилия Джека оказались напрасными.
Коническая Frustum
Усеченный конус — это часть твердого тела, которая остается, когда конус рассекается двумя параллельными плоскостями. Этот калькулятор рассчитывает объем специально для правильного кругового конуса. Типичные конические усики, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы для питья. Объем усеченного правого конуса рассчитывается по следующей формуле:
| объем = | πh (r 2 + rR + R 2 ) |
где r и R — радиусы оснований, h — высота усеченного конуса
EX: Би успешно приобрела мороженое в сахарном рожке и только что съела его так, что мороженое остается упакованным внутри рожка, а поверхность мороженого находится на уровне и параллельно плоскости отверстия рожка.Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть дна ее рожка, которая идеально параллельна ранее единственному отверстию. У Би теперь остается конусообразная усеченная вершина, из которой вытекает мороженое, и ей необходимо рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченной кости 4 дюйма с радиусом 1,5 дюйма и 0,2 дюйма:
объем = 1/3 × π × 4 (0,2 2 + 0,2 × 1,5 + 1,5 2 ) = 10.849 из 3
Эллипсоид
Эллипсоид является трехмерным аналогом эллипса и представляет собой поверхность, которую можно описать как деформацию сферы посредством масштабирования элементов направления. Центр эллипсоида — это точка, в которой пересекаются три попарно перпендикулярные оси симметрии, а отрезки линии, ограничивающие эти оси симметрии, называются главными осями. Если все три имеют разную длину, эллипсоид обычно называют трехосным.Уравнение для расчета объема эллипсоида выглядит следующим образом:
, где a , b и c — длины осей
EX: Хабат любит есть только мясо, но его мать настаивает на том, что он ест слишком много, и позволяет ему есть столько мяса, сколько он может уместить в булочке в форме эллипса. Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может уместить в своем сэндвиче. Учитывая, что его булочка имеет длину оси 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат рассчитывает объем мяса, который он может уместить в каждой полой булочке, следующим образом:
объем = 4/3 × π × 1.5 × 2 × 5 = 62,832 дюйма 3
Квадратная пирамида
Пирамида в геометрии — это трехмерное твердое тело, образованное путем соединения многоугольного основания с точкой, называемой его вершиной, где многоугольник — это форма на плоскости, ограниченная конечным числом отрезков прямой. Есть много возможных многоугольных оснований для пирамиды, но квадратная пирамида — это пирамида, в которой основание представляет собой квадрат. Другое отличие пирамид заключается в расположении вершины. У правых пирамид есть вершина, которая находится прямо над центром тяжести ее основания.Независимо от того, где находится вершина пирамиды, если ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды может быть записан как:
Объем обобщенной пирамиды:
.Калькулятор трубки
Форма трубки
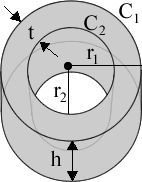
r 1 = внешний радиус
C 1 = внешняя окружность
L 1 = площадь внешней поверхности
V 1 = объем в пределах C 1
r 2 = внутренний радиус
C 2 = внутренняя окружность
L 2 = площадь внутренней поверхности
V 2 = объем в пределах C 2
h = высота
t = толщина стенки
В = объем твердого тела
A = площадь торцевой поверхности
π = пи = 3.1415926535898
√ = квадратный корень
Использование калькулятора
Этот калькулятор рассчитает различные свойства трубы, также называемой трубой или полым цилиндром, по 3 известным значениям из переменных радиуса, окружности, толщины стенки и высоты. Сплошная геометрическая труба обычно представляет собой цилиндр с торцевым профилем, представленным кольцевое пространство.
Единицы: Обратите внимание, что единицы показаны для удобства, но не влияют на вычисления. Единицы измерения указывают порядок результатов, например футы, футы 2 или футы 3 . Например, если вы начинаете с мм и знаете r и h в мм, ваши вычисления приведут к C в мм, V в мм 3 , L в мм 2 и A в мм 2 .
Ниже приведены стандартные формулы для трубки.Вычисления основаны на алгебраическом манипулировании этими стандартными формулами.
Формулы трубки по радиусу и высоте, r и h:
- Окружность, C:
- обычно C = 2πr, следовательно,
- С 1 = 2πr 1
- С 2 = 2πr 2
- Площадь боковой поверхности, L, для
цилиндр:
- обычно L = C * h = 2πrh, следовательно,
- L 1 = 2πr 1 h, площадь внешней поверхности
- L 2 = 2πr 2 h, площадь внутренней поверхности
- Площадь, A, для концевого сечения трубы:
- обычно A = πr 2 , для круг, следовательно,
- А 1 = πr 1 2 для участка, ограниченного C 1
- А 2 = πr 2 2 для территории, ограниченной C 2
- A = A 1 — A 2 для площади сплошного поперечного сечения трубки, на конце.
- А = π (r 1 2 — r 2 2 )
- Объем, В, для
цилиндр:
- обычно V = A * h = πr 2 h, следовательно,
- В 1 = πr 1 2 ч для объема, заключенного в C 1
- В 2 = πr 2 2 ч для объема, заключенного в C 2
- V = V 1 — V 2 для объема твердого тела, трубки.
- В = π (r 1 2 — r 2 2 ) ч
- Толщина стенки трубы, т:
Список литературы
Калькулятор Суп: Калькулятор цилиндров и Калькулятор кольцевого пространства
.Калькулятор площади, объема и наклонной высоты конуса
Решенный пример
Приведенный ниже пример решенной задачи может быть полезен для понимания того, как значения используются в математических формулах для определения площади, объема и высоты наклона правильного кругового конуса.
Пример задачи:
Найти площадь, объем и наклонную высоту правого кругового конуса с радиусом основания и высотой 15 см и 7 см соответственно?
Решение:
Приведенные значения
радиус основания r = 15 см
высота h = 7 см
Пошаговый расчет Формула
для определения площади = πr [r + √ (r 2 + h 2 )]
подставляем значения
= π x 15 x [15 + √ (15 2 + 7 2 )]
= 1487.49 см 2
формула для определения объема = (1/3) π r 2 h
замените значения
= (1/3) x π x 15 2 x 7
= 1650 см 3
Площадь, объем и наклонная высота конуса могут потребоваться для расчета в системе СИ, метрической или стандартной системе единиц США, поэтому в этом калькуляторе конуса предусмотрена функция преобразования основных единиц измерения для нахождения выходных значений в различных стандартных единицах. такие единицы, как дюймы (дюймы), футы (футы), метры (м), сантиметры (см) и миллиметры (мм), используя приведенную ниже таблицу преобразования.
| 10 мм = 1 см 100 мм = 3,93 дюйма 1000 мм = 3,28 фута 1000 мм = 1 м | 1 см = 10 мм 10 см = 3,93 дюйма 100 см = 3,28 фута 100 см = 1 м | 1 фут = 3048 мм 1 фут = 304,8 см 1 фут = 12 дюймов 10 футов = 3,048 м | 1 дюйм = 25,4 мм 1 дюйм = 2,54 см 100 дюймов = 8,33 фута 100 дюймов = 2,54 м |
В области расчетов геометрии определение площади, объема и высоты наклона конуса очень важно для понимания части базовой математики.Приведенные выше формулы, пошаговый расчет и решенный пример могут помочь пользователям понять, как рассчитать площадь, объем и наклонную высоту конуса вручную, однако, когда дело доходит до онлайн-выполнения быстрых вычислений, этот калькулятор конуса может быть полезен. чтобы найти результаты. .