Уклон 0 005: Уклоны канализационных труб. Минимальный и максимальный уклон
Уклон канализационной трубы: минимальный, максимальный
В большинстве случаев канализацию делают самотечной. Это значит, что все стоки уходят самостоятельно, под действием гравитационных сил. Но чтобы они двигались, трубы необходимо укладывать не ровно, а с наклоном, причем с определенным.Каким должен быть уклон канализационных труб и будем говорить дальше.
Ровно канализационные трубы укладывать нельзяСодержание статьи
Для чего нужен уклон канализационной трубы
Все наверное, слышали, что трубы канализации необходимо укладывать с уклоном, да еще при том определенным строительными нормами — СНиПом. Почему именно так? Потому что необходимо чтобы скорость движения стоков по трубам была такой, чтобы вода и твердые частицы двигались вместе.
При самостоятельной прокладке или ремонте существующей канализации часто делаю две ошибки:
Нормы, указанные в СНиПе, носят рекомендательный характер, но они написаны исходя из многолетнего опыта, так что имеет смысл прислушаться.
Какой должен быть уклон
Как понять, что такое уклон трубы? В СНиПе он прописан в долях — в виде десятичных добей. Выгладит это так: 0,03 или 0,008. Расшифровываются цифры так: это разница высот двух концов метрового куска уложенной канализационной трубы. Цифра 0,03 обозначает, что один конец метровой трубы приподнят на 3 см. Соответственно, цифра 0,008 говорит о том, что один край приподнят на 0,8 см или на 8 мм.
Рекомендованный уклон канализационной трубы разного диаметра (50 мм, 100 мм, 150 мм)Трубопровод обычно намного длиннее одного метра. Вычислить насколько один его конец должен быть выше другого, можно умножив выбранный уклон на длину трубопровода. Например, укладывать будем канализацию с уклоном 3 см/м, длина ее — 25 м. Это значит, что дальний конец ее будет опущен на 3 см * 25 м = 75 см.
Зависимость от диаметра трубы
Канализационные системы делят на внутренние — смонтированные в квартире или доме, и внешние — которые уложены на улице. И в том и в другом случае необходимо выдерживать требуемый уклон канализационной трубы.
| Диаметр канализационных труб | Нормальный уклон | Наименьший допустимый |
|---|---|---|
| 50 мм | 0,035 (3,5 см) | 0,025 (2,5 см) |
| 100 мм | 0,02 (2 см) | 0,012 (1,2 см) |
| 150 мм | 0,01 (1 см) | 0,07 (7 мм) |
| 200 мм | 0,008 (0,8 см) | 0,005 (0,5 см) |
В таблице указан уклон канализационной трубы, который обеспечит нормальную работу системы. Если по каким-то причинам сделать требуемый угол наклона не получается (бывает на участках со сложным рельефом), можно угол уклона уменьшать до указанной граничной нормы. Шанс получить проблемы возрастает, но не сильно.
Что делать, если уклон получается больше чем требуется
Иногда сделать требуемый уклон не получается — разные бывают условия. В таком случае есть два варианта решения:
В таком случае есть два варианта решения:
Первый вариант более дешевый в устройстве, но он предполагает частые засоры в трубах. Конечно, при интенсивном использовании канализации (большое количество воды), проблем может и не быть, все может работать без проблем. Но это — скорее исключение. Кстати, при использовании пластиковых труб вероятность засоров становится ниже — они имеют гладкие стенки, на которых осадки образуются редко. Второй вариант — более затратный трудоемкий, но он гарантирует работоспособность системы.
Как выдержать требуемый уклон
Определиться с углом уклона канализации недостаточно. Его еще при прокладке надо выдержать. Самый удобный вариант — наличие специального уровня с угломером. Если профессионального оборудования нет, придется хитрить.
Строительный уровень с угломеромЕсть способы контролировать угол канализационной трубы при помощи обычного уровня:
- Нарисовав на стене линию с желаемым уклоном, прикладываете к ней строительный уровень, делаете на пластике отметку в том месте, где находится край пузырька.
 При выставлении труб располагаете их так, чтобы пузырек оказался в нужном положении.
При выставлении труб располагаете их так, чтобы пузырек оказался в нужном положении. - Если взять метровый уровень, можно с одной стороны прикрепить подкладку требуемой ширины. На котортких участках такой способ не работает, но протяженный трубопровод выставлять удобно.
Внутренняя канализация
При прокладке трубопровода надо выдерживать заданный уклон, не допустить прогибов и провисаний. Кстати, при укладке отводных труб от разных сантехнических приборов требуется выдерживать разные уклоны (смотрите фото ниже).
При прокладке внутреннего трубопровода можно начертить требуемые уклоны на стене, по ним выставить трубы. На уровень пола ориентироваться не стоит, лучше отбить горизонтальную линию. Проще это сделать при наличии нивелира, если его нет, можно пользоваться пузырьковым уровнем. После этого, высчитав требуемый перепад (описано выше), «задираете» дальний конец. Еще раз проверяете точность расчетов и нанесенных линий. После можно приступать к монтажу.
После этого, высчитав требуемый перепад (описано выше), «задираете» дальний конец. Еще раз проверяете точность расчетов и нанесенных линий. После можно приступать к монтажу.
В ванных и туалетах обычно выкладывают требуемый уровень при помощи густого песко-цементного раствора. Все равно потом труба отделывается — ставится короб из гипсокартона, на который затем наклеивается плитка. Более современный вариант — укладывать трубы в штробу доступен не всем — в панельных домах нет такой толщины стен. При прокладке канализационных труб от кухни чаще пользуются подставками и клиньями. После уложенный с требуемым уклоном трубопровод фиксируется к стенам при помощи специальных держателей. Их устанавливают с шагом не более 40 см.
Совет! При монтаже разворачивайте раструбы канализационных против хода потока. Так меньше вероятность получить подтекающие стыки.
Наружная канализация
Канализация на участке укладывается в траншеи. Прокладывая трассу, старайтесь ее сделать как можно более прямой. Любые повороты — потенциальное место образования засора. Если без поворотов обойтись никак не получится, рядом с ним установите тройник, выведите трубу чуть выше уровня грунта и заглушите ее герметичной крышкой. Это будет верное решение — сможете быстро и без проблем прочищать пробки.
Прокладывая трассу, старайтесь ее сделать как можно более прямой. Любые повороты — потенциальное место образования засора. Если без поворотов обойтись никак не получится, рядом с ним установите тройник, выведите трубу чуть выше уровня грунта и заглушите ее герметичной крышкой. Это будет верное решение — сможете быстро и без проблем прочищать пробки.
При прокладке внешней канализации копают траншею с ровным дном. Глубина траншеи — на 20 см больше необходимой — это место под песчаную подушку. При небольшой протяженности и малом перепаде дно можно так и оставить — ровным. Если перепад большой, придется формировать уклон. На этом этапе слишком выдерживать наклон нет необходимости — делаете приблизительно. Затем дно выравнивают, убирают все камни, корни, сравнивают ямы, уплотняют. Должно быть ровное плотное основание.
На выровненное дно насыпают песка. Его надо сыпать слоями по 5 см, разравнивать по уровню, уплотнять (проливать большим количеством воды). Послойно уложив 4 слоя, получаем подушку в 20 см. В песок укладывают трубы, формируя заданный уклон. Уклон можно проверять длинным строительным уровнем (1,5-2 метра или больше). Если такого нет, можно к длинной ровной рейке (брусу) примотать посередине скотчем пузырьковый уровень. Так можно добиться минимальной погрешности.
Послойно уложив 4 слоя, получаем подушку в 20 см. В песок укладывают трубы, формируя заданный уклон. Уклон можно проверять длинным строительным уровнем (1,5-2 метра или больше). Если такого нет, можно к длинной ровной рейке (брусу) примотать посередине скотчем пузырьковый уровень. Так можно добиться минимальной погрешности.
После того как труба уложена и проверен ее уклон, ее засыпают песком. Он должен закрывать ее практически на половину. Песок аккуратно выравнивают и проливают. После этого труба на 1/3 засыпана плотным песком (можно чтобы уровень был больше). Дальше можно засыпать грунтом.
Уклон канализационной трубы на 1 метр: СНиП и угол уклона
Расчет и устройство канализации выполняются с соблюдением необходимых нормативов. Только так вы получите эффективно работающую и долговечную систему. Особенно важно соблюдать уклон канализационной трубы при устройстве самотёчной системы (именно такой вариант удаления стоков используется в квартире и частном доме). Этот параметр зависит от диаметра и длины канализации. Он выбираться согласно СНиП 2.04.03-85 и 2.04.01-85. Недостаточный, как и чрезмерный, уклон труб может привести к множеству проблем. В нашей статье мы расскажем, какой нужен наклон внутренней и наружной канализации, как делать его расчет и на что обращать внимание.
Этот параметр зависит от диаметра и длины канализации. Он выбираться согласно СНиП 2.04.03-85 и 2.04.01-85. Недостаточный, как и чрезмерный, уклон труб может привести к множеству проблем. В нашей статье мы расскажем, какой нужен наклон внутренней и наружной канализации, как делать его расчет и на что обращать внимание.
Особенности определения превышения
Чтобы определить минимальный уклон канализации, домашние мастера пользуются следующими методами:
- Чтобы не делать расчет, некоторые мастера стараются выполнить угол наклона как можно больше.
- Некоторые умельцы вообще упускают этот момент или делают минимальное превышение, которое оговорено в СНиП для трубопроводов другого диаметра.
- Чтобы правильно определить уклон канализационной трубы, нужно сделать специальный расчет, руководствуясь нормативами из СНиП и других регламентирующих документов.
Как может показаться, слишком большой уклон канализационного трубопровода поможет стокам быстрее стекать в общедомовую систему. Однако при очень быстром течении стоков они не успевают смыть все твердые частицы, и те откладываются на внутренней поверхности, образуя засор. Кроме этого, при большой скорости стоки перекрывают весь просвет изделия и вызывают срыв гидрозатвора в сифонах. В итоге газы из канализации проходят в помещение. Именно поэтом даже максимальный наклон трубопровода строго ограничивается СНиП.
Однако при очень быстром течении стоков они не успевают смыть все твердые частицы, и те откладываются на внутренней поверхности, образуя засор. Кроме этого, при большой скорости стоки перекрывают весь просвет изделия и вызывают срыв гидрозатвора в сифонах. В итоге газы из канализации проходят в помещение. Именно поэтом даже максимальный наклон трубопровода строго ограничивается СНиП.
Важно: запрещено делать уклон трубопровода канализации больше чем 150 мм на погонный метр.
Отсутствие наклона или наименьший уклон канализационной трубы может привести к заиливанию трубопровода. Такая система не сможет очищаться естественным путём во время течения воды. В итоге она будет регулярно засоряться и требовать ремонта, что значительно снизит продолжительность службы всей канализации.
Внимание: чтобы канализация прослужила вам без поломок и как можно дольше, необходимо делать предварительный расчет с учётом норм из СНиП, согласно которым превышение подбирается в зависимости от диаметра и протяжённости трубы.
Назначение
Угол наклона канализационной трубы делается при монтаже внутренней и наружной системы в квартире и доме, потому что благодаря этому можно застраховаться от многих проблем в ходе эксплуатации сетей:
Официальное приложение от букмекерской конторы 1xBet, абсолютно бесплатно и скачать 1хБет можно перейдя по ссылке и делать ставки на спорт.- Если система заилится из-за недостаточного уклона или его отсутствия, то просвет канализации сузится, и при сливании большого количества воды будет возникать гидроудар, срывающий гидрозатворы в сифонах. Если в сифоне не будет гидрозатвора, неприятные канализационные газы начнут проникать в помещение квартиры.
- Заиливание магистрального трубопровода будет приводить к выходу всей системы из строя.
- Нормативный уклон канализационной трубы позволит защитить от прорывов и протечек, образующихся в подвале доме.
- Если без наклона установить чугунные элементы канализации, подверженные коррозии, то в системе могут образовываться свищи и прорехи из-за застоя воды.

Важно: наклон трубопровода нужен, чтобы получить оптимальную скорость перемещения сточных вод, при которой твёрдые частицы будут транспортироваться к конечной точке без оседания на дне изделия. Согласно нормам СНиП скорость течения стоков по системе должна быть 0,7 м/сек.
Выбор оптимальной величины
Чтобы произвести расчет необходимого превышения, нужно знать протяжённость всего трубопровода и его назначение. Чтобы не делать расчёт, можно воспользоваться готовыми таблицами из СНиП, где даётся нормативный наклон для сливных систем от разных санитарно-технических приборов:
Рекомендуем к прочтению:
- Для слива от ванной используют элементы 40-50 мм. Максимальное расстояние от слива до сифона без вентиляции – 1 … 1,3 м. Наклон – 1 к 30.
- Слив от душа должен быть выполнен из патрубков 40-50 мм. Максимальное расстояние –1,5 … 1,7 м. Превышение – 1 к 48.
- Слив от унитаза делают из трубопровода размером 10 см.
 Максимальное расстояние – до 6 м. Наклон должен быть 1 к 20.
Максимальное расстояние – до 6 м. Наклон должен быть 1 к 20. - Раковина: элементы размером 40-50 мм, расстояние – 0 … 0,8 м, превышение – 1 к 12.
- Биде: изделия диаметром 30-40 мм, расстояние – 0,7 … 1 м, наклон – 1 к 20.
- Мойка: трубопровод диаметром 30-40 мм, расстояние – 1,3 … 1,5 м, превышение – 1 к 36.
Комбинированный слив от мойки, душа и ванной делается из изделий с размером 5 см. При этом максимальное расстояние должно быть не больше 1,7 … 2,3 м, а наклон – 1 к 48.
Также нормируется оптимальный и минимальный уклон для труб определённого диаметра, подключаемых к конкретным приборам:
- Трубопровод диаметром 4-5 см, идущий от раковины, может иметь минимальный уклон 0,025 промилле, а оптимальной считается 0,35 промилле.
- Изделия сечением 10 см, идущие от унитаза, должны иметь минимальный наклон 0,012, а оптимальный – 0,02.
- Элементы размером 5 см, проложенные от мойки, могут иметь минимальное превышение 0,025, а оптимальная величина равна – 0,035.

- От умывальника и ванной прокладываются трубы сечением 4-5 см с минимальным наклоном 0,025 и оптимальным – 0,035.
Превышение на погонный метр
Как правило, уклон канализации на 1 метр согласно СНиП определяется не в градусах, а в величине, которая выражается в соотношении превышения одного конца трубопровода над другим к погонному метру длины.
Чтобы вы знали, какой уклон труб делать на погонный метр, можете воспользоваться следующими данными:
- Для элементов сечением 50 мм минимальная величина равна 0,03 промилле, то есть один край метрового изделия должен быть выше второго на 30 мм.
- Трубопровод диаметром 110 мм должен иметь превышение, равное 0,02. Это значит, что один край выше другого на 20 мм при длине 1 метр.
- Трубопровод сечением 160 мм должен иметь минимальный наклон 0,008 промилле. Значит, превышение метрового участка составляет 8 мм.
- Элементы с размером 200 мм должны иметь превышение 0,007 промилле, то есть один конец метрового отрезка выше другого на 7 мм.

Важно: чем больше диаметр трубопровода, тем меньше величина превышения.
Чтобы произвести расчет уклона канализационного трубопровода определённой длины, необходимо минимальный наклон, который определяется с учётом сечения элемента, умножить на её общую протяжённость. Например, начало элемента диаметром 110 мм протяжённостью 10 м должно быть выше конца на 20 см, поскольку 10 м х 0,02 (минимальный наклон для трубопровода сечением110 мм) = 0,2 метра или 20 см.
Наружные сети
Определяя уклон канализации в частном доме, стоит не забывать и о наружной сети, которая должна монтироваться с наклоном для удаления сточных вод самотёком. Обычно для прокладки наружных сетей используются изделия большего диаметра, чем внутри дома. При определении наклона руководствуются следующими нормами:
Рекомендуем к прочтению:
- Если будут укладываться элементы диаметром 150 мм, то рекомендуемый наклон равен 0,008 промилле. Если по каким-то причинам не получится соблюдать такое превышение, то можно его уменьшить до величины 0,007.

- В случае укладки трубопровода сечением 200 мм минимальное превышение должно составлять 0,007 промилле. Оно может быть уменьшено при необходимости до 0,005.
Также нормируется и показатель максимального уклона наружного трубопровода. Для элементов любого диаметра он не может быть более 0,15, то есть превышение не больше 15 см. С большим наклоном система не сможет правильно функционировать, поскольку будут образовываться засоры.
Расчет наполняемости
При выполнении расчета обязательно находится наполняемость трубопровода. Эта величина поможет определить скорость движения стоков, которая очень важна для нахождения оптимального превышения, при котором система сможет эффективно функционировать.
Важно: для определения наполняемости уровень воды в трубе нужно разделить на диаметр трубопровода. Минимальная наполняемость согласно нормам равна 0,3, а максимальная – 1.
Получив уровень расчётной наполняемости, необходимо использовать проверочную формулу, то есть сравнить полученное значение с коэффициентом оптимальной наполняемости для элементов из определённых материалов:
- для пластиковых и стеклянных изделий он равен 0,5;
- для систем из чугуна, асбестоцемента и керамики эта величина равна 0,6.

Для сравнения из полученной расчётной величины берётся квадратный корень и умножается на минимальную скорость движения стоков, которая равна 0,7 м/с. Полученное число нужно сравнить с оптимальной наполняемостью системы (исходя из материала). Оно должно быть больше либо равно ему.
Уклон 0 005 — Портал о стройке
Содержание статьи:
Наклон крыши и его значение при строительстве домов
Проезжая мимо населенных пунктов, мы часто рассматриваем крыши домов и построек. Одни похожи на крутые склоны Эльбруса, другие — на покатые спуски дальневосточных сопок. Почему же перекрытия имеют такой разный наклон? Уклон кровли способствует быстрому удалению атмосферных осадков с территории сооружения и измеряется углом между плоскостью ската крыши и плоскостью горизонта. Чем больше величина угла ската, тем круче крыша, и наоборот, с его уменьшением крыша становится более покатистая или пологая, пока не перейдет в горизонтальную. Этот угол профессионалы архитектурного строительства измеряют градусами (º), процентами (%) или числовым соотношением. Если угол очень маленький, тогда используют измерение в промилле (сотых долях процента). Для справки: 1º — 1,7%; 1% — 34′ 20″.
Этот угол профессионалы архитектурного строительства измеряют градусами (º), процентами (%) или числовым соотношением. Если угол очень маленький, тогда используют измерение в промилле (сотых долях процента). Для справки: 1º — 1,7%; 1% — 34′ 20″.
Наклон любой крыши является очень важным элементом. Его величина вычисляется в зависимости от климата и применяемого кровельного материала.
Наклон плоскости любой части крыши является очень важным элементом при домостроении, и его величина выбирается в зависимости от климата и применяемого кровельного материала. Он влияет на ее надежность, герметичность, на возможность водоотвода, а значит, и на долговечность здания в целом. Для правильного выбора материала кровли, а также для расчета его расхода, высоты сооружения нужно знать, как посчитать уклон кровли.
Виды крыш и выбор их материала
Виды формы крыш.
Для каждого здания уклон крыши рассчитывается индивидуально.
Различают 4 вида крыш:
- высокие;
- скатные;
- пологие;
- плоские.

Плоские перекрытия не являются абсолютно горизонтальными, а имеют угол наклона, но он не менее 3º, при этом крыша обустраивается специальными водоотводными воронками с уклоном стенок около 1,5º.
При эксплуатации на поверхность кровли оказывает давление ветер, поэтому высокие более подвержены этому воздействию, а с очень пологих крыш ураган может сорвать кровельное покрытие.
Угол наклона крыши зависит от материала, выбранного для кровли, а также плоскости ската.
С увеличением размера угла наклона от 11º до 45º это давление усиливается почти в 5 раз. Учитывая ветровые нагрузки, на местностях с несильными ветрами этот размер выбирают в пределах 35-40º, а там, где скорость движения воздушных масс высока, — 15-25º.
Следует отметить, что при больших значениях угла наклона плоскости перекрытия (около 50º) зимой снег будет съезжать с нее под собственным весом, сводя к нулю его давление на кровлю.
От крутизны плоскости ската зависит выбор материала, а иногда и количество его слоев при укладке.
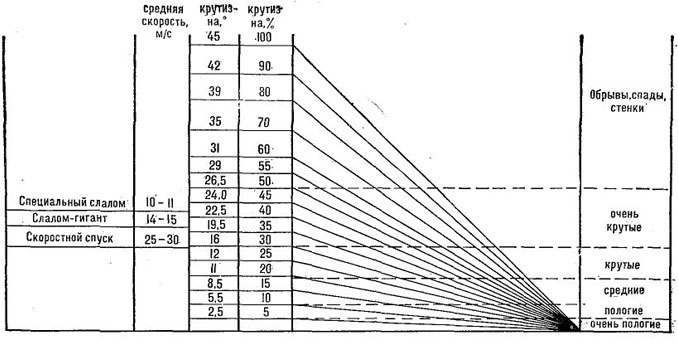
Диаграмма связывает минимальный наклон крыши с кровельным материалом и помогает в выборе при необходимости и того, и другого. Вертикальная шкала обозначает уклон в процентах, дуговидная — в градусах, на полках указано соотношение высоты к заложению. Материал условно сгруппирован по своим технико-экономическим свойствам в 11 категорий.
Практика показывает, что рулонные материалы применяют для накрытия кровель с уклоном 0-25% (0-10% — трехслойное покрытие, 10-25% — однослойное покрытие, но материал должен быть с посыпкой). Асбестоцементный шифер укладывают на крышах с наклоном до 28%, стальные листы — до 29%, черепица — более 33%.
Вычисление угла ската к горизонту
Его можно просто измерить уклономером, который являет собой планку с рамкой с маятником со стрелкой, показывающей градусную величину. Но на сегодняшний день этот прибор уже неактуален, поскольку есть много капельных и электронных уклономеров с намного большей точностью измерения и удобством пользования.
Расчет угла наклона крыши.
При отсутствии в распоряжении геодезических устройств для измерения существует простой математический метод, позволяющий относительно точно посчитать угол наклона стропил. Для этого используется рулетка и отвес. От конька до перекрытия здания опускается отвес и измеряется высота h. Затем от точки, в которой отвес касался перекрытия под коньком, измеряем расстояние до нижней точки ската — заложение l.
Угол наклона крыши зависит от выбранного для кровли материала.
Угол наклона ската i равен отношению высоты конька к заложению (при одинаковых единицах измерения) і = h:l. При этом уклон выражен соотношением, которое показывает, на какую высоту поднимается кровля на протяжении единицы заложения (на сколько метров будет поднят верхний край крыши на одном метре горизонтального перекрытия). Чтобы посчитать этот же уклон в процентах, умножаем полученное соотношение на 100%. Если же нужно знать эту величину в градусах, переводим ее с помощью таблицы.
Для примера: высота кровли h = 3,0 м, длина заложения l=6,5 м. Тогда і = h:l = 3,0:6,5 = 1:2,17. Это пример измерения уклона соотношением. і = 3,0:6,5 = 0,4615. В процентном измерении это значение вычисляется умножением его на 100%: і = 0,4615. 100% = 46,15%. Для определения угла в градусах переводим по таблице и получаем 25º. Если есть нужда в более точном градусном значении, тогда из полученного соотношения, применяя калькулятор или специальные таблицы, вычисляем котангенс, который будет равен 24,78º.
Следует отметить, что уклон в 100% — это когда высота кровли равна заложению, то есть соответствует соотношению 1:1 или углу наклона в 45º. Но не следует думать, что процентная величина уклона и его градусная величина имеют прямую зависимость. Ведь уклон в процентах — это значение тангенса угла при нижней точке ската, умноженное на 100%, а график тангенса (тангенсоида) никогда не был прямой линией. И если 100% — это 45º, то 50% — это не 22,5º, а около 27º (точнее 26,56º).
youtube.com/embed/kpnzjnJhgbQ&feature=share&list=PLxGukzvbwLed88MOnNdM0yBnuDYcVUW8H&index=4″/>
Практическое применение результатов вычисления
Кроме того что угол уклона позволяет выбрать материал кровли, он необходим при промежуточных вычислениях в процессе строительства дома. Зная значения угла в процентах, можно посчитать высоту конька. Для этого заложение умножаем на уклон h = l х і = 6,5 х 0,46 = 2,99 м. Либо зная уклон и высоту, можно посчитать расстояние до нижней точки ската l = h : і = 3,0 : 0,46 = 6,52 м. Точность полученных линейных размеров зависит от точности измерений и вычислений. В данном случае невысокая точность вычислений (до сотых) дает расхождение в пределах 1-2 см. Измерение угла ската кровли в процентах намного удобнее при строительстве крыши, чем в градусах.
Source: 1metallocherepica.ru
Читайте также
Как правильно выставить уклон канализации на 1 метр СНиП
Грамотный монтаж канализационной системы невозможен без предварительных расчетов. Необходимо определить диаметр труб, скорость движения стоков и уклон канализации на 1 метр СНиП. Ошибки при выборе последнего параметра могут вызвать существенные проблемы в работе автономной канализации.
Что такое угол наклона трубопровода?
Монтаж труб канализации не должен выполняться по горизонту, а находится к нему под небольшим углом, значение которого определяют специальные нормативы. Для обозначения уклона трубы используется не привычная система градусов, здесь коэффициент определяется в сантиметрах на метр. Такая размерность позволяет избежать больших погрешностей при монтаже магистрали к септику. Длина такой ветки может составлять 10-12 метров и выдержать заданный угол очень сложно. Предложенное обозначение показывает – насколько один конец трубы длиной в 1 метр должен быть выше другого.
Внимание. В справочной литературе уклон трубы обозначается простой или десятичной дробью. Например, коэффициент 0,03 означает уклон 3 см на 1 метр.
Соотношение диаметров труб и рекомендуемого уклона
Кроме рекомендованного уклона канализации на 1 метр, норматив определяет максимальный и минимальный показатель.
Максимальный уклон
Верхняя граница допустимого значения не должна превышать 0,15, это означает наклон погонного метра трубы на 15 см. Больший коэффициент может использоваться на коротких участках, примыкающих к сантехническим приборам. Необходимо учитывать скорость потока, она не может быть больше 1,4 м/с, иначе твердые фракции осядут на стенках магистрали. Сточные воды состоят из многочисленных взвесей и частиц с различной вязкостью и текучестью. При уклоне, превышающем 15 см, они расслаиваются — жидкость уходит в септик, а оставшиеся фракции заиливают трубу.
Минимальный уклон
Минимальный показатель определен для каждого сечения трубы:
- 50 мм – 0,025;
- 100 мм – 0,012;
- 150 мм – 0,007;
- 200 мм – 0,005.
При несоблюдении этих показателей трубопровод быстро забьется. На отдельных участках, протяженностью не более 1 метра, допускается коэффициент 0,01.
Ошибки при выборе угла наклона труб
Нормальное функционирование системы отведения загрязненных вод обеспечивает сила тяжести, жидкость движется по трубам самотеком. При неверном выборе угла наклона возникают следующие сбои:
- Недостаточный уклон канализации – сточные воды двигаются медленно и застаиваются в трубе, что приводит к образованию засора. Особенно губительно такое явление для чугунных магистралей, которые подвергаются усиленной коррозии, возникают порывы и протечки.
- Большой угол наклона – ускорение потока приводит к недостаточной очистке труб, вода быстро уходит, а крупные фракции остаются на стенках. Работа такой магистрали сопровождается шумом и срывом водных затворов на сифонах.
Рекомендуемый коэффициент уменьшается с возрастанием диаметра трубы:
- 40-50 мм – 0,03;
- 100 мм – 0,02;
- 150 мм – 0,008;
- 200 мм – 0,007.
Ошибки при монтаже трубопровода
Как рассчитать степень наполненности трубопровода
Для стабильной работы канализации важны такие показатели:
- скорость течения стоков V;
- наполнение канализационной системы K.
K=H/D,
H – высота уровня сточных вод;
D – сечение канализации.
Рассчитав уровень наполненности магистрали, можно определить оптимальную скорость потока, при которой система будет функционировать без заиливания и мусорных засоров. Полная наполненность тубы составляет 1, при этом нарушается вентиляция системы, и могут сорваться гидрозатворы. Эффективный показатель составляет 0,5-0,6, если он опускается до 0,3, то жидкости недостаточно для смыва твердых фракций. Этот коэффициент зависит от материала труб, гладкий пластик имеет меньшую наполняемость, чем шероховатый чугун и асбестоцемент.
Совет. Описание последовательности расчетов и необходимые формулы берутся из СНиП 2.04.01-85.
Формула для расчета уклона труб
Скорость течения сливаемых отходов является ключевым параметром при вычислении оптимального уклона канализационной трубы. Ее минимальное значение составляет 0,7 м/с. Выполнить расчет для индивидуальной системы можно по формуле:
V√(H/d)≥K,
K – наполнение трубы, для полимерных материалов коэффициент – 0,5, для чугуна – 0,6;
d – сечение трубы;
V – скорость потока.
Из формулы следует, что соотношение скорости движения канализационных стоков к наполненности магистрали не должна быть меньше коэффициента K. В случае H/d=0 – канализация пуста, и скорость потока рассчитать невозможно.
Рекомендации по монтажу внутренней системы канализации
В квартирах и внутренней разводке частного дома используются трубы небольшого диаметра, кроме подключения унитаза. Уклон канализационной трубы 50 мм, используемой для ванны, раковины и душа, составляет 3 см на каждый метр. При монтаже магистрали длиной в 10 метров, ее самая высокая точка должна находиться в 30 см от самой низкой. Устраивая самостоятельно разводку, необходимо действовать согласно правилам:
- для горизонтальных труб не допускаются повороты в 90º, нужно устанавливать два фасонных элемента по 45º;
- соединение вертикальных участков под прямым углом допускается нормативами;
- исключаются изменения в типе канализационной разводки на ее различных участках, это приведет к выходу из строя всей системы в результате возникновения гидроударов;
- на отдельных частях магистрали, имеющих небольшое расстояние, возможно увеличение уклона больше максимальной нормы.
Схема размещения сантехники с уклоном труб
Угол уклона для наружной инженерной сети
Наружные сети монтируются из труб большего сечения, чем внутридомовая разводка. Материалом для них служит:
- полиэтиленовая труба с верхним гофрированным слоем;
- пластик;
- чугун;
- асбестоцемент.
Их установка согласно нормам СНиП должна учитывать уровень промерзания почвы. Глубина траншеи может составлять от 70 см в средней полосе до 2 метров в холодных регионах. В местах поворота трубопровода и при длине магистрали более 12 метров, необходимо устанавливать ревизионные колодцы, эти элементы позволят прочистить засоры в системе.
Для загородного дома с двумя санузлами используется трубами диаметром 110 мм, если в доме три туалета и более, рекомендуется прокладка трубопровода сечением 160 мм. При выкапывании траншеи оставляется запас до 20 см для выравнивания трубы до рекомендуемого угла уклона. Каждый размер магистрали имеет свой рекомендованный коэффициент уклона:
- 110 мм – 0,02 или 2 см на 1 метр;
- 160 мм – 0,008 или 8 мм на 1 метр.
Совет. При монтаже наружной магистрали следует ограничить число поворотов, увеличивающих угол наклона. Из-за рельефа могут возникнуть сложности с обеспечением необходимого уклона.
Прокладывание наружной магистрали
Соблюдение нормативов позволяет сохранять работоспособность магистрали при движении нечистот самотеком. Оптимальным прибором для определения правильного уклона является нивелир, используя его можно добиться высокой точности. Но такое устройство есть не у всех, поэтому найдены способы проверки с помощью подручных средств. Для измерения понадобится:
- шнур или веревка;
- два колышка;
- строительный уровень.
В прокопанной траншее забиваются колышки – один в начале, а второй в конце. Между ними натягивается шнур и с помощью строительного уровня выставляется по горизонту. Затем измеряется глубина траншеи до шнура в начальной точке и в конечной. Разница между этими значениями, деленная на длину трубопровода должна составить искомую величину наклона канализационной трубы на 1 погонный метр. Подогнать значение под нужный показатель, можно углубив или подсыпав песок на дно. Укладка труб всегда выполняется на подушку из утрамбованного песка. Этим же материалом выполняется первоначальная засыпка до верха магистрали, а после выполняется обратная засыпка грунта.
Если природный рельеф участка существенно превышает нормативный показатель, можно смонтировать магистраль двумя способами:
- создать систему, включающую несколько вертикальных переходов и горизонтальных участков, уложенных с рекомендованным уклоном;
- выкопать глубокую траншею, в которой разместится один вертикальный отрезок в начале трубопровода, остальная часть будет уложена по нормативному уклону.
Соблюдение правильного уклона при монтаже трубопровода внутри и снаружи частного дома обеспечит бесперебойную работу автономной канализации.
стандарты и технологии || СанТехМонтаж
Через систему внутренней канализации сточная вода выводится из здания и с помощью наружного трубопровода транспортируется дальше по сети в септики или резервуары-накопители. Чтобы автономная канализация справлялась с поставленными задачами, необходимо правильно выполнить прокладку канализационной системы. Устанавливается она с наклоном, направленным от выпуска из здания в сторону септика. Только правильный монтаж сможет обеспечить бесперебойную утилизацию отходов жизнедеятельности.
Угол снижения канализационной системы
Уклон магистрали – это показатель, без которого невозможно грамотно обустроить слив стоков. Эта величина установлена в СНиП, для расчета применяются специальные формулы.
Уклон обеспечивает самоочищение трубопровода, он зависит от размера сечения. Для каждого диаметра предусмотрен свой минимальный показатель понижения.
Если наклон недостаточный, то нечистоты будут застаиваться, что приведет к образованию засоров. При слишком крутом снижении утилизируемые воды будут быстро стекать, оставляя тяжелые фракции на дне. Это часто становится причиной оседания и накапливания ила на стенках трубопровода, от этого канализационная система быстро засоряется, ее срок службы снижается.
Правила монтажа наружной канализации
Наполненность – это ключевая величина для укладки магистрали. Для определения этой характеристики используется формула:
y = H/d
- d – это сечение;
- H – уровень утилизируемых жидких сред.
Скорость течения жидких сред должна быть выше 0,7 м/с, а уровень — 1/3 от диаметра.
Рассчитывается скорость перемещения бытовых отходов, при которой происходит самоочищение, таким образом:
V√ H/d≥K
- V – скорость перемещения жидких сред;
- H/d – наполняемость;
- K – коэффициент сопротивляемости, на который влияет материал трубы.
Но если использовать эту формулу невозможно, то применяются нормативы. Для выполнения работ по строительству разработан стандарт СНиП, принятый в 1985 году. В нем расписан механизм вычисления угла снижения трубопровода и определены необходимые условия для наружной сети. Этим справочником руководствуются при проектировании самотечных магистралей.
СНиПом установлено, что для наружной канализации лучше использовать трубы диаметром более 110 мм, а на всем протяжении рекомендуется соблюдать уклон 0,02 м/пог.м.
Трубы d 160 мм укладываются с наклоном 0,008 – 0,007 м на метр проложенной магистрали, для d 200 мм — 0,007 – 0,005 м. Чем ближе показатели угла снижения к нормативным, тем лучше магистраль будет действовать.
Наибольшим значением, при котором все будет работать корректно, является 0,15 (15 см на каждый метр трубопровода).
Но если нет под рукой СНиП или других законодательных актов, то рассчитать минимальную величину снижения можно так:
Y = 1/ID
- здесь Y – минимальный показатель угла снижения;
- ID – внутренний d трубы.
Чтобы определить, какая будет разница между крайними точками трубопровода, нужно знать его длину. Тогда уклон трассы рассчитывается так:
U = L * Y
- U – общий наклон;
- L – длина;
- Y – минимальный показатель наклона.
Этот расчет показывает общее понижение магистрали.
При проектировании нужно также учитывать и другие особенности сети, такие как характер нагрузки. Если вода стекает из умывальника, то вероятность заиливания маленькая и уклон можно сделать круче рекомендованного.
К кому обратиться за помощью?
Ваша заявка успешно отправлена!
Сеть, проложенная с соблюдением строительных требований, сохранит наклон, а сточные воды протекут по трубе и попадут в септик. Корректный расчет и правильная установка канализационной сети избавят от проблем и дополнительных хлопот.
Монтаж канализации требует наличия специальных знаний и навыков. Поэтому устройство канализационной сети лучше доверить профессионалам.
Наша компания реализует и выполняет монтаж автономных канализаций – септиков Биопурит в Нижнем Новгороде и области, мы также устанавливаем канализационные системы для частных домов и загородных коттеджей.
Обращайтесь в нашу компанию, и мы сделаем все, чтобы все сроки договора были соблюдены, система прослужила долго, а цены были в пределах бюджета.
Расчет и нанесение уклона на обмерных чертежах
С необходимостью посчитать уклон постоянно сталкиваются проектировщики, строители, архитекторы, а также люди ряда других профессий, в силу того, что на земной поверхности очень трудно найти идеально ровный участок. Уклон выражается в градусах или в процентах. Обозначение в градусах показывает угол кривизны поверхности. Но уклон может быть представлен и в виде тангенса этого угла, умноженного на 100%.
Как рассчитать уклон поверхности?
Уклон – это отношение превышения (ВС) к заложению (АС) и обозначается в текстовых документах буквой i.
Например, i=1:6
Разделите противолежащий катет (вертикальное расстояние) на прилежащий (расстояние между точками). Если вам нужно получить уклон в процентах, умножьте полученное число на 100%. Чтобы получить уклон в промилле, умножьте результат деления на 1000‰.
Если вам необходимо получить уклон в градусах, воспользуйтесь тем, что полученный при делении катетов результат – тангенс угла наклона. Посчитайте его арктангенс при помощи инженерного калькулятора, в результате вы получите значение уклона в градусах.
На видах (фасадах), разрезах, сечениях и схемах перед размерным числом, определяющим величину уклона, наносят знак , острый угол которого должен быть направлен в сторону уклона.
Обозначение уклона наносят непосредственно над линией контура или на полке линии-выноски.
На планах направление уклона плоскостей указывают стрелкой, на которой, при необходимости, проставляют величину уклона (см.рис.).
Построение и обозначение уклона. Пример изображения уклона на планах.
Величину уклона (тангенс угла наклона) указывают в виде простой или десятичной дроби с точностью до третьего знака.
Уклон (в строительстве) — показатель крутизны склона (а также ската кровли).
Укло́н (в геодезии) — показатель крутизны склона; отношение превышения местности к горизонтальному проложению, на котором оно наблюдается. Иными словами, величина уклона равна тангенсу угла между поверхностью склона и горизонталью.
Уклон поверхности равен тангенсу угла α, tgα = h/l — отношение перпендикуляра, опущенного из точки поверхности на прямую поверхность, к длине прямой поверхности от начала склона (при вершине угла α) до перпендикуляра.
Например, подъёму 12 м на 100 м перемещения по горизонтали соответствует уклон, равный 0,12 (12 % или 120 ‰).
При чтении нотации знак «%» произносится «сотых», а «‰» — «тысячных».
Источник:
книга: Единые требования по выполнению строительных чертежей.
М.: Изд-во «Архитектура-С», 2004.
Справочное пособие.
Автор: Георгиевский О.В.
Аннотация:
Справочное пособие по строительному черчению для студентов средних и высших учебных заведений. Пособие выполнено в соответствии с требованиями ГОСТов.
Настоящее справочное пособие выполнено в соответствии с требованиями ГОСТов ЕСКД (Единой системы конструкторской документации) и СПДС (Системы проектной документации для строительства).
Пособие может быть использовано при выполнении заданий по архитектурно-строительному черчению, а также при выполнении курсовых и дипломных проектов студентами всех строительных специальностей средних и высших учебных заведений.
распечатать
Вконтакте
Одноклассники
Google+
Уклон — газопровод — Большая Энциклопедия Нефти и Газа, статья, страница 1
Уклон — газопровод
Cтраница 1
Уклоны газопроводов необходимо увязывать с рельефом местности. Если уклон совпадает с направлением движения газа, то его величину мож-но уменьшать. В соответствии с требованиями Правил Госгортехнадзора минимально допустимый t уклон составляет 0 0015 или 1 5 мм на каждый метр длины газопровода. [1]
Уклон газопровода к стояку и приборам ( кроме счетчика) для труб диаметром до 32 мм делают 0 ОС2н — 0 005 мм, а для труб диаметром 40 — 75 мм — 0 008 — 0 015 мм. [2]
Уклоны газопроводов от стояка в сторону ввода и приборов должны составлять 2 — 5 мм на 1 м трубопроводов. При установке газовых счетчиков уклоны газопроводов должны быть выдержаны в указанных пределах от счетчика к стояку и от счетчика к приборам. [3]
Уклоны газопроводов от стояка в сторону ввода и приборов должны составлять 2 — 5 мм на I м трубопроводов. При установке газовых счетчиков уклоны газопроводов должны быть выдержаны в указанных пределах от счетчика к стояку и от счетчика К приборам. [4]
Уклоны газопроводов от стояка в сторону ввода и приборов должны составлять 2 — 5 мм на 1 м трубопроводов. При установке газовых счетчиков уклоны газопроводов должны быть выдержаны в указанных пределах от счетчика к стояку и от счетчика к приборам. [5]
Уклон газопроводов должен быть от счетчика к газовому вводу и от счетчика к газовым агрегатам. [6]
Уклоны газопровода соответствуют проекту. [7]
Если уклон газопровода идет против направления течения газа в трубе, то величина уклона должна быть несколько больше, чем в тех случаях, когда направление уклона совпадает с направлением течения газа. [8]
Внутри жилых зданий уклон газопроводов должен быть от счетчика к стояку и от счетчика к газовым приборам; в котельных и помещениях коммунально-бытовых потребителей уклон делают от счетчика к газовому вводу и от счетчика к газовым приборам. [9]
Для беспрепятственного стока конденсата уклон газопровода должен приниматься в пределах 0 005 — 0 009; в пониженных точках линии следует установить дрйпы для конденсата. [10]
Для экономии земляных работ уклоны газопроводов желательно по возможности приспособить к рельефу поверхности улиц. [11]
Для экономии земляных работ уклоны газопроводов желательно по возможности приспосабливать к рельефу поверхности улиц. [12]
При наличии газовых счетчиков уклон газопровода должен быть от счетчика к стояку или вводу и от счетчика к газовым приборам. [13]
Это рас-зтояние зависит от уклона газопровода, скорости газового потока и количества имеющейся в газопроводе жидкости и должно определяться практическим путем, исходя из конкретных условий. [14]
Какое значение имеют постель и уклоны газопроводов. [15]
Страницы: 1 2 3
3Устный наклон | Макроэкономика
Цели обучения
- Как различать положительные и отрицательные отношения
Рисунок 1 .Этот лыжник ускоряется вниз по склону в олимпийских гонках. Что вы думаете о крутизне или наклоне этого горнолыжного холма?
Что означает наклонКонцепция наклона очень полезна в экономике, поскольку она измеряет взаимосвязь между двумя переменными. Положительный наклон означает, что две переменные положительно связаны — то есть, когда x увеличивается, увеличивается y , а когда x уменьшается, y также уменьшается.Графически положительный наклон означает, что по мере того, как линия на линейном графике перемещается слева направо, линия поднимается. В других разделах мы узнаем, что «цена» и «поставленное количество» имеют положительную связь; то есть фирмы будут поставлять больше, когда цена выше.
Рисунок 1. Положительный наклон.
Отрицательный наклон означает, что две переменные связаны отрицательно; то есть, когда x увеличивается, y уменьшается, а когда x уменьшается, y увеличивается.Графически отрицательный наклон означает, что по мере того, как линия на линейном графике перемещается слева направо, линия падает. Мы узнаем, что «цена» и «количество спроса» имеют отрицательную связь; то есть потребители будут покупать меньше, когда цена будет выше.
Рисунок 2. Отрицательный наклон.
Наклон нуля от нуля означает, что y является постоянным независимо от значения x . Графически линия плоская; превышение пробега равно нулю.
Рисунок 3. Наклон нуля
График уровня безработицы на Рисунке 4 ниже иллюстрирует общий образец многих линейных графиков: некоторые сегменты, где наклон положительный, другие сегменты, где наклон отрицательный, и еще другие сегменты, где наклон близок к нулю.
Рисунок 4. Уровень безработицы в США, 1975–2014 гг.
Расчет уклона
Наклон прямой между двумя точками можно рассчитать численно. Чтобы рассчитать уклон, начните с обозначения одной точки в качестве «начальной точки», а другую точку — в качестве «конечной точки», а затем рассчитайте превышение пробега между этими двумя точками.
Попробуй
Используйте график, чтобы найти наклон линии.
Рисунок 5.
Начать с точки на линии, например [latex] (2,1) [/ latex], и двигаться вертикально, пока не совпадет с другой точкой на линии, например [latex] (6,3) [/ latex] . Подъем 2 единицы. Это положительно по мере вашего продвижения.
Затем двигайтесь по горизонтали до точки [latex] (6,3) [/ latex]. Подсчитайте количество единиц. Пробег 4 единицы. Это положительно, когда вы переместились вправо.
Затем решите по формуле:
[латекс] \ displaystyle \ text {Slope} = \ frac {\ text {rise}} {\ text {run}} [/ latex]
так
[латекс] \ displaystyle \ text {Slope} = \ frac {2} {4} = \ frac {1} {2} [/ latex]
Попробуй
Эти следующие вопросы позволят вам получить столько практики, сколько вам нужно, поскольку вы можете щелкнуть ссылку вверху первого вопроса («Попробуйте другую версию этих вопросов»), чтобы получить новый набор вопросов. Практикуйтесь, пока не почувствуете себя комфортно, задавая вопросы, а затем двигайтесь дальше.
Графики экономических отношений не всегда прямые. В этом курсе вы часто будете видеть нелинейные (изогнутые) линии, как на рисунке 6, который показывает взаимосвязь между количеством производимой продукции и стоимостью ее производства. По мере увеличения объема выпуска общие затраты увеличиваются более быстрыми темпами. Таблица 1 показывает данные, стоящие за этим графиком.
| Таблица 1: Кривая общих затрат | ||
| Объем выпуска (кв.) | Общая стоимость (TC) | |
| 1 | $ 1 | |
| 2 | $ 4 | |
| 3 | $ 9 | |
| «Точка А» | 4 | $ 16 |
| «Точка Б» | 5 | $ 25 |
| 6 | $ 36 | |
| 7 | $ 49 | |
| 8 | $ 64 | |
| 9 | $ 81 | |
| 10 | $ 100 | |
Рисунок 6. В этом примере общие затраты на производство увеличиваются более быстрыми темпами, когда увеличивается объем выпуска.
Мы можем интерпретировать нелинейные отношения так же, как мы интерпретируем линейные отношения. Их наклоны могут быть как положительными, так и отрицательными. Аналогичным образом мы можем рассчитать наклоны, глядя на подъем на отрезке кривой.
В качестве примера рассмотрим наклон кривой общих затрат, приведенный выше, между точками A и B. При переходе от точки A к точке B рост — это изменение общих затрат (т. Е.е. переменная по вертикальной оси):
25–16 долларов = 9
долларовАналогично, пробег — это изменение количества (т. Е. Переменная на горизонтальной оси):
5–4 = 1
Таким образом, наклон прямой между этими двумя точками будет 9/1 = 9. Другими словами, когда мы увеличиваем количество продукции, произведенной на одну единицу, общие затраты на производство увеличиваются на 9 долларов.
Предположим, что наклон линии увеличивается. Графически это означает, что будет круче.Предположим, что наклон линии должен уменьшаться. Тогда стало бы лестнее. Эти условия верны независимо от того, был ли наклон положительным или отрицательным с самого начала. Более низкий положительный наклон означает более пологий наклон кривой вверх, что вы можете видеть на Рисунке 6 при низких уровнях вывода. Более высокий положительный наклон означает более крутой наклон кривой вверх, который вы можете увидеть при более высоких уровнях выходного сигнала.
Отрицательный наклон, который больше по абсолютной величине (т. Е. Более отрицательный), означает более крутой наклон линии вниз.Нулевой наклон — это горизонтальная линия. Вертикальная линия имеет бесконечный наклон.
Предположим, линия имеет больший отрезок. Графически это означает, что он сместится (или вверх) от старого источника параллельно старой линии. Это показано на Рисунке 7 ниже, как сдвиг от линии с меткой Y к линии с меткой Y 1 . Если линия имеет меньшую точку пересечения, она сместится внутрь (или вниз) параллельно старой линии.
Рис. 7. При большем пересечении оси Y весь график смещается в сторону пересечения оси Y в более высокой точке.
Глоссарий
- отрицательный наклон:
- указывает, что две переменные связаны отрицательно; когда одна переменная увеличивается, другая уменьшается, а когда одна переменная уменьшается, другая увеличивается
- положительный наклон:
- указывает, что две переменные положительно связаны; когда одна переменная увеличивается, увеличивается и другая, а когда одна переменная уменьшается, другая также уменьшается
- наклон:
- изменение вертикальной оси, деленное на изменение горизонтальной оси
- наклон нуля:
- указывает на отсутствие связи между двумя переменными; когда одна переменная изменяется, другая не меняется
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
Разница между неопределенным наклоном и нулевым наклоном (с таблицей) — спросите любую разницу
С математической точки зрения подъем или пробег между любыми двумя точками на определенной линии называется наклоном. Наклон в основном используется для измерения крутизны конкретной линии. Он состоит из двух точек или координат. Эти точки часто обозначаются переменными, буквами «X» и «Y». Изменение одной из переменных повлияет на другую и наоборот.
Буквы «X» и «Y» имеют две разные оси. На этих осях с помощью целых чисел ставятся линии и точки. Эти целые числа могут быть как положительными, так и отрицательными, причем ноль всегда находится в центре графика. Ноль всегда лежит на пересечении этих двух осей.
Очень часто используется понятие откосов. Эта концепция используется в разных сферах. Это понятие используется в таких областях, как экономика, строительство, архитектура и т. Д. Поля, связанные со здоровьем и анализом тенденций, также используют понятие наклона в своей повседневной деятельности.По сути, все, что использует угол или крутизну, можно измерить с помощью формулы для уклона.
В большинстве случаев наклон выражается положительными или отрицательными целыми числами. Хотя в некоторых случаях значение как «X», так и «Y» может быть равно нулю. В таких случаях возникает неопределенный нулевой наклон, в котором числитель или знаменатель равен нулю.
Неопределенный и нулевой наклонРазница между неопределенным наклоном и нулевым наклоном состоит в том, что неопределенный наклон означает, что он имеет вертикальную линию, тогда как, с другой стороны, горизонтальная линия имеет нулевой наклон.Ноль является знаменателем неопределенного наклона, а ноль — числителем нулевого наклона.
Основные различия между неопределенным наклоном и нулевым наклоном| Параметр сравнения | Неопределенный наклон | Угол наклона нуля | Характеристики не определены вертикальная линия. | Характеристики нулевого наклона — горизонтальная линия. |
| Значение | Неопределенный наклон имеет несуществующее значение, поскольку не может иметь никакого конкретного значения. | Нулевой наклон имеет нулевое значение, которое определяется. | ||
| Определители | Неопределенный наклон определяется переменной «X». | Нулевой наклон определяется переменной «Y». | ||
| Ноль | Неопределенный наклон имеет нулевой знаменатель. | Нулевой наклон имеет нулевое значение в качестве разницы между его числителями. | ||
| Изменить | При неопределенном наклоне «X» не изменяется, а «Y» изменяется. | При нулевом наклоне «Y» не меняется, тогда как «X» изменяется. |
Проще говоря, Неопределенный наклон можно определить как прямую линию на любом графике. По сути, это наклон вертикальной линии.В неопределенном уклоне переменная «X» не имеет существующего значения. Это не определено. Знаменатель неопределенного наклона равен нулю. Именно по этой причине значение этого наклона не существует независимо от числителя. Поскольку числитель нельзя разделить на ноль, значение всегда не существует.
Неопределенный наклон представлен переменной «X». Разница между двумя точками «X» равна нулю. Любая линия на этом наклоне не перемещается ни влево, ни вправо по переменной «Y»., поскольку по горизонтали нет изменений. Переменная «Y» не изменяется в случае неопределенного наклона, тогда как переменная «X» изменяется.
Что такое нулевой наклон?Проще говоря, нулевой наклон — это наклон горизонтальной линии. Горизонтальная линия на графике характеризуется как нулевой наклон. Он представлен переменной «Y». Переменная «Y» не изменяется, тогда как переменная «X» продолжает изменяться в случае нулевого наклона.
Числитель нулевого наклона всегда равен нулю.Таким образом, разница между двумя точками по переменной «Y» равна нулю. Независимо от знаменателя значение нулевого наклона равно нулю. Таким образом, уклон становится определенным числом. Это потому, что числитель равен нулю, и когда ноль делится на любое число, результат равен нулю. Нулевой наклон — это, по сути, прямая линия, которая не движется вверх или вниз по направлению к переменной «X». Эта линия проходит параллельно переменной «X».
Основные различия между неопределенным наклоном и нулевым наклоном- В случае неопределенного наклона график линии вертикальный, тогда как при нулевом наклоне график линии горизонтален.
- В случае неопределенного наклона знаменатель равен нулю, тогда как в случае нулевого наклона разница между числителями равна нулю.
- Значение неопределенного наклона не определено и не существует. С другой стороны, в случае нулевого наклона значение наклона определяется и равно нулю.
- Неопределенный наклон представлен переменной «X», тогда как, с другой стороны, нулевой наклон представлен переменной «Y».
- Неопределенный наклон выполняется параллельно переменной «Y», тогда как, с другой стороны, нулевой наклон выполняется параллельно переменной «X».
- В случае неопределенного наклона переменная «X» остается постоянной, тогда как переменная «Y» изменяется. С другой стороны, в случае нулевого наклона переменная «Y» остается постоянной, тогда как переменная «X» изменяется.
Концепция склонов очень широко используется в повседневной деятельности. Наклоны представлены переменными «X» и «Y». Наклоны представлены целыми числами, которые могут быть как положительными, так и отрицательными. Однако в некоторых случаях переменные «X» и «Y» могут быть равны нулю или могут отсутствовать.В таких случаях числитель или знаменатель равны нулю. Эти случаи называются неопределенным уклоном или нулевым уклоном.
Неопределенный наклон и Нулевой наклон отличаются друг от друга, поскольку Неопределенный наклон представлен переменной «X», тогда как, с другой стороны, нулевой наклон представлен переменной «Y». Неопределенный наклон представляет собой вертикальную линию, а нулевой наклон — горизонтальную линию.
Ссылки- https://link.springer.com/content/pdf/10.1007 / s11053-005-6951-3.pdf
- https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/JB076i008p01905
Значение производной
5
Скорость изменения функции
при определенном значении x
Уклон прямой
Наклон касательной к кривой
Секущая кривой
Коэффициент разницы
Определение производной
Производная от f ( x ) = x 2
Различается при x
Обозначения для производной
Простой коэффициент разности
Раздел 2: Проблемы
Производная от f ( x ) = 2 x — 5
Уравнение касательной к кривой
Производная от f ( x ) = x 3
РАСЧЕТ ПРИМЕНЯЕТСЯ К ВЕЩАМ, которые не изменяются с постоянной скоростью.Скорость из-за силы тяжести, рождений и смертей в популяции, единицы y для каждой единицы x . Значения функции, называемой производной, будут иметь переменную скорость изменения.
Теперь, поскольку мы считаем x независимой переменной, а y зависимой, то любое изменение Δ x в значении x приведет к изменению Δ y в значении . y . В прямой линии скорость изменения — такое количество единиц на на каждую единицу x — постоянна и называется наклоном линии.
Наклон прямой такой номер:
| Δ y Δ x | = | = | Изменение в и -кладе Изменение в x -кординате | . |
(Тема 8 Precalculus.)
Прямая линия имеет один и только один наклон; одна и только одна скорость изменения.
Если, например, x представляет время, а y представляет расстояние, тогда
прямолинейный график, который их связывает, указывает на постоянную скорость. Скажем, 45 миль в час — в каждый момент времени.
Наклон касательной к кривой
Исчисление, однако, связано со скоростью изменения, которая не является постоянной.
Если эта кривая представляет расстояние Y в зависимости от времени X , то скорость изменения — скорость — в каждый момент времени непостоянна.Вопрос, который задает расчет: «Какова скорость изменения точно в точке P ?» Ответом будет наклон касательной к кривой в этой точке. И метод определения этого наклона — этого числа — был замечательным открытием Исаака Ньютона (1642-1727) и Готфрида Лейбница (1646-1716). Это метод нахождения того, что называется производной.
Секущая кривой
Касательная — это прямая линия, которая только касается кривой.Секущая — это прямая линия, пересекающая кривую. Следовательно, рассмотрим секущую линию, которая пересекает кривую в точках P и Q . Тогда наклон секущей равен
| Δ y Δ x | = |
Но еще раз вопрос, который задает исчисление: как функция изменяется точно при x 1 ?
Каков наклон касательной к кривой на P ?
Однако мы не можем оценить точно при P — потому что Δ y и Δ x тогда оба будут равны 0, а значение будет совершенно неоднозначным.
Поэтому мы будем рассматривать более короткие и более короткие расстояния Δ x , что приведет к последовательности секущих —
— череда спусков. И мы определим касательной в точке P как предел этой последовательности наклонов.
Этот наклон, этот предел будет значением того, что мы будем называть производной.
Коэффициент разницы
Пусть y = f ( x ) будет непрерывной функцией, и пусть координаты фиксированной точки P на графике будут ( x , f ( x )). (Тема 4 Precalculus.) Пусть теперь x изменится на величину Δ x . Тогда новый x -кординат будет x + Δ x .
Это x -координат Q на графике.
Но когда значение x изменяется, возникает результирующее изменение Δ y
в значении y , то есть в значении f ( x ). Его новое значение — f ( x + Δ x ). Координаты Q следующие ( x + Δ x , f ( x + Δ x )).
Затем
Итак, это определение наклона касательной в точке P :
Наклон касательной на P
— это предел изменения функции (числитель)
, деленный на изменение независимой переменной
, когда это изменение приближается к 0.
Поскольку Δ x , а не x — это переменная, которая приближается к 0, x остается постоянным, и этот предел будет функцией x . Поскольку она будет производной от f ( x ), мы называем ее производной функцией или производной от f ( x ). Чтобы напомнить нам, что он был производным от f ( x ), мы обозначим его как f ‘ ( x ) — « f-prime из x .«
Это частное —
— называется частным Ньютона, или разностным коэффициентом. Его вычисление и упрощение — фундаментальная задача дифференциального исчисления.
Опять же, коэффициент разности является функцией Δ x . Но для упрощения записанных вычислений вместо Δ x будем писать h .
| Δ x | = | ч |
| Δ y | = | f ( x + h ) — f ( x ) |
Тогда коэффициент разницы будет:
Теперь сформулируем определение производной следующим образом.
ОПРЕДЕЛЕНИЕ 5. Под производной функции f ( x ) мы подразумеваем следующий предел, если он существует:
Мы называем это ограничение функцией f ‘ ( x ) — « f -prime x » — и когда этот предел существует, мы говорим, что f само по себе является дифференцируемым при x . , и что f имеет производную.
Итак, мы берем предел коэффициента разницы, равный h , приближающемуся к 0.Когда этот предел существует, это означает, что коэффициент разницы можно сделать настолько близким к этому пределу — « f ‘ ( x )» — как нам угодно. (Урок 2.)
Что касается x , мы должны считать его фиксированным. Это конкретное значение, при котором мы оцениваем f ‘ ( x ).
На практике мы должны упростить коэффициент разности, прежде чем позволить h приблизиться к нулю. Мы должны выразить числитель —
f ( x + h ) — f ( x )
— таким образом, чтобы мы могли разделить его на h .
Подводя итог: производная — это функция — правило, которое присваивает каждому значению x наклон касательной в точке ( x , f ( x )) на график f ( x ). Это скорость изменения f ( x ) в этот момент.
В качестве примера мы применим определение, чтобы доказать, что наклон касательной к функции f ( x ) = x 2 , в точке ( x , x 2 ), это 2 x .
| ТЕОРЕМА. | f ( x ) | = | x 2 |
| означает | |||
| f ‘ ( x ) | = | 2 х . | |
Доказательство. Вот коэффициент разницы, который мы продолжим для упрощения:
| 1) | ( x + h ) 2 — x 2 h | |
| 2) | = | x 2 + 2 xh + h 2 — x 2 h |
| 3) | = | 2 xh + h 2 h |
| 4) | = | 2 x + h . |
При переходе от строки 1) к строке 2) мы возводим в квадрат бином x + h . (Урок 18 алгебры.)
В строке 3) мы вычли x 2 с. То есть мы вычли f ( x ).
В строке 4) мы разделили числитель на h . (Урок 20 из Алгебра.)
Мы можем это сделать, потому что h никогда не равно равному 0, даже если мы берем предел (Урок 2).
Завершим определение производной и возьмем предел:
| f ‘ ( x ) | = | (2 x + h ) | |
| = | 2 х . | ||
Это то, что мы хотели доказать.
Всякий раз, когда мы применяем определение, мы должны алгебраически манипулировать коэффициентом разности, чтобы мы могли просто заменить h на 0. Фактически, вся теория пределов со всеми ее сложностями и тонкостями была изобретена, чтобы оправдать именно это. (Бедного Ньютона и Лейбница критиковали за то, что они предлагали оправдания, которые не нравились изобретателям ограничений в XIX веке.) Мы можем положить здесь h = 0, потому что коэффициент разности уменьшается до 2 x + h и, следовательно, многочлен от h .
Проблема. Пусть f ( x ) = x 2 , и вычислим наклон касательной к графику —
a) при x = 5.
Поскольку f ‘ ( x ) = 2 x , то при x = 5 наклон касательной составляет 10.
б) при x = −3. −6.
c) при x = 0.0.
Различается при x
Согласно определению, функция будет дифференцируемой при x , если там существует определенный предел. Графически это означает, что график при этом значении x будет иметь касательную линию. Тогда при каких значениях функция , а не будет дифференцируемой?
Без касательной
Выше два примера.Функция слева не имеет производной при x = 0, потому что там функция является разрывной. При x = 0 тангенса, очевидно, нет.
Что касается графика справа, это функция абсолютного значения, y = | x |. (Тема 5 Precalculus.) И невозможно определить касательную линию при x = 0, потому что график образует там острый угол. Фактически, наклон касательной, когда x приближается к 0 слева, равен -1.Однако наклон, приближающийся справа, равен +1. Наклон касательной при 0, который был бы производной при x = 0, поэтому не существует. (Определение 2.2.)
Функция абсолютного значения, тем не менее, является непрерывной при x = 0. Так, левый предел самой функции, когда x приближается к 0 , равен , равному правому пределу, а именно 0. Это иллюстрирует эту непрерывность. в точке не является гарантией дифференцируемости — существования касательной — в этой точке.
(И наоборот, если функция дифференцируема в точке — если есть касательная — она также будет непрерывной там. График будет гладким и без изломов.)
Поскольку дифференциальное исчисление — это изучение производных, оно в основном занимается функциями, которые дифференцируемы при всех значениях их областей определения. Такие функции называются дифференцируемыми.
Можете ли вы назвать элементарный класс дифференцируемых функций?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала подумайте об этом сами!
Полиномы.
Обозначения для производной
Поскольку производной является этот предел: тогда символ самого лимита (читается: «dee- y , dee- x .»)
Например, если
| y | = | x 2 , | |
| затем, как мы видели, | |||
| = | 2 х . | ||
«Dee- y , dee- x — производная от y по отношению к x — это 2 x .»
Пишем еще
y ‘ ( x ) = 2 x .
« y — простое число x равно 2 x .»
| Сам по себе символ: | d dx | («dee, dee- x «) | , называется |
дифференцирующий оператор .Мы должны взять производную от того, что следует за ней.
Например,
| d dx | f ( x ) означает производную по отношению к x от f ( x ). |
| d dt | (4 т 3 -5) означает производную по отношению к т |
| из (4 т 3 -5). |
И так далее.
Простой коэффициент разности
Коэффициент разницы является версией. И иногда мы будем использовать последнее. То есть изменение значения функции y = f ( x ) равно y + Δ y . Следовательно, коэффициент разницы составляет
Иногда бывает удобно выразить коэффициент разницы как
Примечание : Когда Δ x приближается к 0 — когда точка Q приближается к P вдоль кривой — тогда Δ y или, что эквивалентно, Δ f также приближается к 0.То есть
Теперь ученик должен выполнить Задачи, требующие определения производной.
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставался в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
(Цветной онлайн) Граничная гистограмма наклонов нулевого порядка (слева) и…
Контекст 1
… при этом RMS-высота и RMS-наклон подавляются, что уменьшает количество степеней свободы, и уравнения зависят только от детерминированной переменной v. На рисунке 5 сравнивается маргинальные гистограммы нулевого порядка высот и наклонов освещенных точек, заданные статистической функцией освещения нулевого порядка с корреляцией и без нее и методом Монте-Карло. Масштаб по оси Y изменяется для каждой части рисунка, чтобы четко показать различия….
Контекст 2
… корреляция высот и уклонов не учитывается для упрощения вычислений. На рисунке 5 показано, что учет корреляции значительно улучшает функцию освещения Смита. …
Контекст 3
… в таком случае 4L имеет порядок длины корреляции, что означает, что следует учитывать корреляцию между этими точками. Игнорирование этой корреляции приводит к различию между некоррелированной моделью и результатом Монте-Карло, как показано на рисунке 5….
Контекст 4
… также наблюдается максимум S 1% 0,23, но при% 75. Для больших углов наблюдения (2 [85, 90]) только около 0-10% поверхности испытывает поверхностное отражение. Для поверхности с 0,5 (пунктирная линия и ромбы на рисунке 10) поверхностное отражение широко наблюдается для 2 [0, 90]. …
Контекст 5
… первая задача — определить форму эмпирического фактора. Как мы обсуждали в разделе 4.1, недостатком некоррелированной функции затенения нулевого порядка является то, что пренебрежение корреляцией между высотой и уклоном приводит к равной вероятности освещения для этих точек с 5 (см. Сплошные линии на рисунке 6), что приводит к с расхождением, показанным на рисунках 5 (a) и 5 (c).Фактически, вероятность освещения должна уменьшаться по мере приближения s к v (см. Пунктирные линии на рисунке 6). …
Контекст 6
… эмпирический коэффициент f (пунктирная линия) и числовые образцы f num (разбросанные точки) показаны на рисунке 11 (a). Метод наименьших квадратов выполняется для подбора только тех точек, где f num 51, потому что S 0, MC и S 0, u малы и более или менее одинаковы, когда S 0, MC превышает S 0, u (см. Рисунки 5 (a ) и 5 (в)). Умножение эмпирического коэффициента на коэффициент угловой освещенности некоррелированной функции освещения нулевого порядка приводит к эмпирическому коэффициенту угловой освещенности нулевого порядка, который затем сравнивается с коэффициентом коррелированной функции освещения нулевого порядка….
Контекст 7
… 1 и f (v 1) являются функциями 0, интегрирование по 0 должно выполняться численно. Результаты показаны на Рисунке 15, где снова получены очень хорошие соглашения. …
y перехват | х перехват
Введение ПерехватПересечение — это точка, в которой линия или кривая проходят через ось графика. Когда точка пересекает ось x, эта точка называется пересечением по оси x или горизонтальным пересечением.
И когда эта точка пересекает ось Y, эта точка называется пересечением по оси Y или вертикальным пересечением.
Теперь давайте познакомимся с терминами, используемыми для определения пересечения по горизонтали и по вертикали.
Во-первых, мы должны знать, каково уравнение линии
Уравнение прямой можно записать как \ (y = mx + b \)
Где \ (m \) называется наклоном прямой, а b — точкой пересечения оси y.
Теперь мы должны знать, что подразумевается под наклоном прямой
Наклон линии определяется наклоном или крутизной линии.
Это отношение изменения значения y к изменению значения x.
Это называется «превышение скорости»
\ [Slope = \ frac {\ text {изменение значения y}} {\ text {изменение значения x}} = \ frac {\ rm {rise}} {\ rm {run}} \]
Выше на графике мы можем найти подъем на графике, взяв любые две точки, это 4
Трасса 3, значит, уклон здесь 4/3.
Склоны бывают следующих типов: —
А теперь перейдем к перехвату.
Найти точки пересечения по осям x и yДавайте сделаем пример.
Найдите точки пересечения x и y для прямой 6x + 3y = 18.
Как найти точку пересечения x?
установить y = 0
\ [\ begin {align} 6x + 3 (0) & = 18 \\ 6x & = 18 \\ x & = \ frac {18} {6} \\ x & = 3 \ end {align} \]
Как найти точку пересечения по вертикали?
установить x = 0
\ [\ begin {align} 6 (0) + 3y & = 18 \\ 3y & = 18 \\ y & = \ frac {18} {3} \\ y & = 6 \ end {align} \]
Найдите точки пересечения по осям x и y по графикуТеперь пересечения по осям x и y можно определить, также посмотрев на графики.
Попытайтесь наблюдать приведенный ниже график и найдите точки пересечения по осям x и y.
Как найти точку пересечения по оси x?
Здесь точка пересечения x — это место, где линия пересекает ось x. Он равен -4, поэтому точка пересечения по оси x равна (-4,0)
Перехват по вертикали
Теперь точка пересечения y — это точка, в которой она пересекает ось y.
Он пересекает ось y в точке 6, поэтому точка пересечения y составляет (0,6)
Построение линии путем вычисления пересечений по осям x и y при задании уравнения.Мы также можем построить линии, вычислив точки пересечения. Давайте посмотрим на эту концепцию на примере.
Нарисуйте график 5x + 3y = 15, найдя точки пересечения по осям x и y.
Как найти точку пересечения x?
x пересечение задается установкой y = 0
\ [\ begin {align} 5x = 15 \\ x = \ frac {15} {5} \\ x & = 3 \ end {align} \]
Перехват по вертикали
Y пересечение задается установкой x = 0 в уравнении
\ [\ begin {align} 5 (0) + 3y & = 15 \\ 3y & = 15 \\ y & = 5 \ end {align} \]
Постройте точки пересечения по осям x и y, затем проведите линию
Случаи, когда нет точки пересечения по оси X и точки пересечения по оси YТеперь имейте в виду, что точки пересечения x и y — это не числа, а упорядоченные пары.Предположим, что значение x intercept равно 2, оно записывается как (2,0). Кроме того, не все графики имеют как горизонтальные, так и вертикальные точки пересечения. Например:
Горизонтальная линия на графике выше не имеет точки пересечения по оси x. Он имеет только точку пересечения y как (0, -2).
Теперь давайте рассмотрим случай, когда нет точки пересечения оси y
Вертикальная линия на графике выше имеет точку пересечения по оси x (3,0) и не имеет точки пересечения по оси y.
Теперь случай, когда точки пересечения x и y — это одни и те же точки i.e.origin
График после нахождения пересечений по осям x и y: y = -2x.
Чтобы найти x, перехватить x = 0
Y = -2 (0)
Y = 0
Итак, точка пересечения y равна (0,0)
Чтобы найти точку пересечения с x, положите y = 0
0 = -2x
Х = 0
Таким образом, отрезок x равен (0,0)
Итак, точки пересечения по оси x и по оси y — это на самом деле одни и те же точки, начало координат. Теперь нам нужна еще одна точка для построения графика: линия выбирает любое значение для x и определяет значение для 5
.Если мы возьмем x равным 1, мы получим y = -2
Если мы возьмем x как -1, получим y = 2
Теперь используйте эти упорядоченные пары для построения графика линии (0,0), (- 1,2) (1, -2) для построения графика линии
11.4 Понятие наклона прямой — Предалгебра 2e
Будьте готовы 11.10
Прежде чем начать, пройдите тест на готовность.
Упростить: 1−48−2.1−48−2.
Если вы пропустили эту проблему, просмотрите Пример 4.49.
Будьте готовы 11.11
Делить: 04,40.04,40.
Если вы пропустили эту проблему, просмотрите Пример 7.37.
Будьте готовы 11.12
Упростить: 15−3, −153, −15−3,15−3, −153, −15−3.
Если вы пропустили эту проблему, просмотрите Пример 4.47.
Когда мы рисовали линейные уравнения, мы заметили, что некоторые линии наклонены вверх, когда идут слева направо, а некоторые линии наклонены вниз. Некоторые линии очень крутые, а некоторые более плоские. Что определяет наклон линии вверх или вниз, крутой или плоский?
Крутизна наклона линии называется наклоном линии. Концепция уклона имеет множество применений в реальном мире. Наклон крыши и уклон шоссе или пандуса для инвалидных колясок — это лишь некоторые примеры, на которых вы буквально видите уклоны.А когда вы едете на велосипеде, вы чувствуете наклон при подъеме или спуске по инерции.
Использование географических досок для моделирования откоса
В этом разделе мы исследуем понятие уклона.
Использование резинок на геодлане дает конкретный способ моделирования линий на координатной сетке. Натянув резиновую ленту между двумя колышками на геодоске, мы можем узнать, как найти наклон линии. А когда вы едете на велосипеде, вы чувствуете уклон при подъеме или спуске по инерции.
Манипулятивная математика
Выполнение упражнения по манипулятивной математике «Исследование наклона» поможет вам лучше понять наклон линии.
Начнем с того, что натянем резиновую ленту между двумя колышками, чтобы образовать линию, как показано на рисунке 11.17.
Рисунок 11.17
Это похоже на линию?
Теперь мы растягиваем одну часть резинки прямо вверх от левого стержня и вокруг третьего стержня, чтобы образовать стороны прямоугольного треугольника, как показано на рисунке 11.18. Осторожно делаем угол 90 ° 90 ° вокруг третьего стержня так, чтобы одна сторона была вертикальной, а другая — горизонтальной.
Рисунок 11.18
Чтобы найти наклон прямой, мы измеряем расстояние по вертикальной и горизонтальной сторонам треугольника. Расстояние по вертикали называется подъемом , а расстояние по горизонтали называется отрезком , как показано на рис. 11.19.
Рисунок 11.19
Чтобы лучше запомнить термины, можно подумать об изображениях, показанных на рисунке 11.20.
Рисунок 11.20
На нашей геоборде подъем составляет 22 единицы, потому что резинка поднимается на 22 места на вертикальной опоре. См. Рисунок 11.21.
Какой пробег? Обязательно считайте промежутки между колышками, а не сами колышки! Резинка проходит через 33 места на горизонтальной ноге, поэтому пробег составляет 33 единицы.
Рисунок 11.21
Уклон линии — это отношение подъема к разбегу. Таким образом, наклон нашей линии равен 23,23. В математике наклон всегда обозначается буквой m.м.
Уклон прямой
Уклон линии m = riserun.m = riserun.
Подъем измеряет вертикальное изменение, а бег — горизонтальное изменение.
Каков наклон линии на геоплане на рис. 11.21?
Линия имеет наклон 23 и наклон 23.Когда мы работаем с геобордами, неплохо иметь привычку начинать с колышка слева и соединяться с колышком справа. Затем натягиваем резинку, чтобы получился прямоугольный треугольник.
Если мы начнем с подъема, подъем будет положительным, а если растянуть его вниз, подъем будет отрицательным. Мы будем считать пробег слева направо, как вы читали этот абзац, поэтому пробег будет положительным.
Поскольку в формуле уклона есть подъем за пробегом, может быть проще всегда сначала отсчитывать подъем, а затем разбег.
Пример 11.30
Каков наклон линии на геоданге?
Решение
Используйте определение наклона.
м = стояк
Начните с левого стержня и сделайте прямоугольный треугольник, потянув резиновую ленту вверх и вправо, чтобы добраться до второго стержня.
Подсчитайте подъем и разбег, как показано.
Подъем составляет 3 единицы. M = 3 пробега. Прогон составляет 4 единицы. M = 34. Наклон составляет 34. Подъем составляет 3 единицы. M = 3 пробега. Прогон составляет 4 единицы. M = 34. Наклон составляет 34.
Попробуй 11,58
Каков наклон линии на геоданге?
Попробуй 11,59
Каков наклон линии на геоданге?
Пример 11.31
Каков наклон линии на геоданге?
Решение
Используйте определение наклона.
м = стояк
Начните с левого колышка и сделайте прямоугольный треугольник, натянув резиновую ленту на колышек справа. На этот раз нам нужно растянуть резинку вниз, чтобы получилась вертикальная штанина, поэтому подъем будет отрицательным.
Подъем -1 м = -1 пробег 3 м = −13 м = −13 Наклон −13 Подъем −1.m = −1run Пробег 3.m = −13m = −13 Наклон −13.
Попробуй 11.60
Каков наклон линии на геоданге?
Попробуйте 11,61
Каков наклон линии на геоданге?
Обратите внимание, что в первом примере наклон положительный, а во втором примере наклон отрицательный. Вы заметили разницу в двух линиях, показанных на рисунке 11.22.
Рисунок 11.22
Если читать слева направо, линия на рисунке A поднимается вверх; имеет положительный наклон.Линия на рисунке B идет вниз; имеет отрицательный наклон.
Рисунок 11.23
Пример 11.32
Используйте географическую доску, чтобы смоделировать линию с уклоном 12.12.
Решение
Чтобы смоделировать линию с определенным уклоном на географической доске, нам нужно знать подъем и уклон.
| Используйте формулу наклона. | м = стояк |
| Заменить мм на 1212. | 12 = riserun12 = riserun |
Итак, прибавка составляет 11 единиц, а пробег — 22 единицы.
Начните с колышка в нижнем левом углу геодоски. Протянуть резинку вверх на 11 единиц, а затем вправо на 22 единицы.
Гипотенуза прямоугольного треугольника, образованного резинкой, представляет собой линию с наклоном 12,12.
Попробуй 11,62
Используйте геоборд, чтобы смоделировать линию с заданным наклоном: m = 13.m = 13.
Попробуй 11,63
Используйте географическую доску, чтобы смоделировать линию с заданным уклоном: m = 32.m = 32.
Пример 11.33
Используйте географическую доску, чтобы смоделировать линию с уклоном −14, −14,
Решение
| Используйте формулу наклона. | м = стояк |
| Заменить мм на −14−14. | −14 = переходник-14 = переходник |
Итак, рост равен -1-1, а разбег равен 4,4.
Поскольку рост отрицательный, мы выбираем начальную отметку в верхнем левом углу, которая даст нам возможность отсчитывать обратный отсчет.Протягиваем резинку вниз на 11 единиц, затем вправо на 44 единицы.
Гипотенуза прямоугольного треугольника, образованного резинкой, представляет собой линию с наклоном -14,14.
Попробуй 11,64
Используйте геодоску, чтобы смоделировать линию с заданным наклоном: m = −21.m = −21.
Попробуй 11,65
Используйте географическую доску, чтобы смоделировать линию с заданным наклоном: m = −13.m = −13.
Найдите наклон прямой по ее графику
Теперь мы посмотрим на некоторые графики на координатной сетке, чтобы найти их наклоны.Этот метод будет очень похож на тот, который мы только что смоделировали на наших геобордах.
Манипулятивная математика
Выполнение упражнения по манипулятивной математике «Наклон линий между двумя точками» поможет вам лучше понять, как найти наклон линии по ее графику.
Чтобы найти наклон, мы должны отсчитать подъем и разбег. Но с чего начать?
Находим любые две точки на прямой. Мы стараемся выбирать точки с координатами, которые являются целыми числами, чтобы упростить наши вычисления.Затем мы начнем с точки слева и нарисуем прямоугольный треугольник, чтобы мы могли посчитать подъем и бег.
Пример 11.34
Найдите наклон показанной прямой:
Решение
Найдите две точки на графике, выбирая точки, координаты которых являются целыми числами. Мы будем использовать (0, −3) (0, −3) и (5,1). (5,1).
Начиная с точки слева, (0, −3), (0, −3), нарисуйте прямоугольный треугольник, идущий от первой точки ко второй точке (5,1).(5,1).
| Посчитайте подъем на вертикальной стороне треугольника. | Подъем 4 шт. |
| Посчитайте пробег на горизонтальной ноге. | Пробег 5 шт. |
| Используйте формулу наклона. | м = стояк |
| Подставьте значения подъема и пробега. | м = 45 м = 45 |
| Уклон линии 4545. |
Обратите внимание, что наклон положительный, поскольку линия наклонена вверх слева направо.
Попробуй 11,66
Найдите наклон прямой:
Попробуйте 11,67
Найдите наклон прямой:
How To
Найдите наклон на графике.
- Шаг 1. Найдите на линии две точки, координаты которых являются целыми числами.
- Шаг 2. Начиная с точки слева, нарисуйте прямоугольный треугольник, идущий от первой точки ко второй.
- Шаг 3. Посчитайте подъем и разбег по сторонам треугольника.
- Шаг 4. Определите отношение подъема к бегу, чтобы найти уклон. m = riserunm = riserun
Пример 11.35
Найдите наклон показанной прямой:
Решение
Найдите две точки на графике. Ищите точки с целыми числами. Мы можем выбрать любые точки, но будем использовать (0, 5) и (3, 3). Начиная с точки слева, нарисуйте прямоугольный треугольник, идущий от первой точки ко второй.
| Посчитайте прибавку — она отрицательная. | Рост на -2. |
| Подсчитайте пробег. | Пробег 3. |
| Используйте формулу наклона. | м = стояк |
| Подставьте значения подъема и пробега. | м = -23 м = -23 |
| Упростить. | м = -23 м = -23 |
| Наклон прямой равен −23.−23. |
Обратите внимание, что наклон отрицательный, так как линия наклонена вниз слева направо.
Что, если бы мы выбрали разные точки? Давайте снова найдем наклон линии, на этот раз используя другие точки. Мы будем использовать точки (−3,7) (- 3,7) и (6,1). (6,1).
Начиная с (−3,7), (- 3,7), нарисуйте прямоугольный треугольник до точки (6,1). (6,1).
| Посчитайте прибавку. | Рост на −6. |
| Подсчитайте пробег. | Пробег 9. |
| Используйте формулу наклона. | м = стояк |
| Подставьте значения подъема и пробега. | м = -69 м = -69 |
| Упростим дробь. | м = -23 м = -23 |
| Наклон прямой равен −23. − 23. |
Неважно, какие точки вы используете — наклон линии всегда один и тот же.Наклон линии постоянный!
Попробуй 11,68
Найдите наклон прямой:
Попробуй 11,69
Найдите наклон прямой:
Строки в предыдущих примерах имели точки пересечения yy с целыми значениями, поэтому было удобно использовать точку пересечения y в качестве одной из точек, которые мы использовали для определения наклона. В следующем примере отрезок yy представляет собой дробь. Расчеты упрощаются, если мы используем две точки с целыми координатами.
Пример 11.36
Найдите наклон показанной линии:
Решение
| Найдите на графике две точки, координаты которых являются целыми числами. | (2,3) (2,3) и (7,6) (7,6) |
| Какая точка слева? | (2,3) (2,3) |
| Начиная с (2,3) (2,3), нарисуйте прямой угол к (7,6) (7,6), как показано ниже. |
| Посчитайте прибавку. | Повышение на 3. |
| Подсчитайте пробег. | Пробег 5. |
| Используйте формулу наклона. | м = стояк |
| Подставьте значения подъема и пробега. | м = 35 м = 35 |
| Наклон линии 35,35. |
Попробуйте 11,70
Найдите наклон прямой:
Попробовать 11,71
Найдите наклон прямой:
Найдите наклон горизонтальных и вертикальных линий
Вы помните, что было особенного в горизонтальных и вертикальных линиях? В их уравнениях была всего одна переменная.
- горизонтальная линия y = b; y = b; все координаты yy совпадают.
- вертикальная линия x = a; x = a; все xx-координаты совпадают.
Итак, как нам найти наклон горизонтальной прямой y = 4? Y = 4? Один из подходов — построить горизонтальную линию, найти на ней две точки и посчитать подъем и пробег. Посмотрим, что происходит на рис. 11.24. Мы будем использовать две точки (0,4) (0,4) и (3,4) (3,4) для подсчета подъема и бега.
Рисунок 11.24
| Какой рост? | Рост 0. |
| Что такое пробег? | Пробег 3. |
| Какой уклон? | м = стояк |
| м = 03 м = 03 | |
| м = 0 м = 0 |
Наклон горизонтальной прямой y = 4y = 4 равен 0,0.
Все горизонтальные линии имеют наклон 00. Если координаты yy совпадают, подъем равен 00.
Наклон горизонтальной линии
Наклон горизонтальной линии y = b, y = b равен 0.0.
Теперь рассмотрим вертикальную линию, например линию x = 3x = 3, показанную на рисунке 11.25. Мы будем использовать две точки (3,0) (3,0) и (3,2) (3,2) для подсчета подъема и бега.
Рисунок 11.25
| Какой рост? | Повышение на 2. |
| Что такое пробег? | Пробег 0. |
| Какой уклон? | м = стояк |
| м = 20 м = 20 |
Но мы не можем разделить на 0.0. Деление на 00 не определено. Итак, мы говорим, что наклон вертикальной прямой x = 3x = 3 не определен. Наклон всех вертикальных линий не определен, потому что пробег равен 0,0.
Наклон вертикальной линии
Наклон вертикальной линии x = a, x = a не определен.
Пример 11.37
Найдите наклон каждой прямой:
- ⓐx = 8x = 8
- ⓑy = −5y = −5
Решение
ⓐx = 8x = 8
Это вертикальная линия, поэтому ее наклон не определен.
ⓑy = −5y = −5
Это горизонтальная линия, поэтому ее наклон равен 0,0.
Попробовать 11,72
Найдите наклон прямой: x = −4.x = −4.
Попробовать 11,73
Найдите наклон прямой: y = 7.y = 7.
Краткое руководство по склонам линий
Используйте формулу наклона, чтобы найти наклон линии между двумя точками
Иногда нам нужно найти наклон линии между двумя точками, и у нас может не быть графика для подсчета подъема и разбега.Мы могли бы нанести точки на сетку, а затем подсчитать подъем и пробег, но есть способ найти наклон без построения графика.
Прежде чем мы перейдем к этому, нам нужно ввести некоторые новые алгебраические обозначения. Мы видели, что упорядоченная пара (x, y) (x, y) дает координаты точки. Но когда мы работаем со склонами, мы используем две точки. Как можно использовать один и тот же символ (x, y) (x, y) для обозначения двух разных точек?
Математики используют индексы, чтобы различать точки.Нижний индекс — это небольшое число, записанное справа от переменной и немного ниже нее.
- (x1, y1) readxsub1, ysub1 (x1, y1) readxsub1, ysub1
- (x2, y2) readxsub2, ysub2 (x2, y2) readxsub2, ysub2
Мы будем использовать (x1, y1) (x1, y1) для идентификации первой точки и (x2, y2) (x2, y2) для идентификации второй точки. Если бы у нас было больше двух точек, мы могли бы использовать (x3, y3), (x4, y4), (x3, y3), (x4, y4) и так далее.
Чтобы увидеть, как подъем и бег связаны с координатами двух точек, давайте еще раз посмотрим на наклон линии между точками (2,3) (2,3) и (7,6) (7,6). ) на рисунке 11.26.
Рисунок 11.26
Поскольку у нас две точки, мы будем использовать индексные обозначения.
(2,3) x1, y1 (7,6) x2, y2 (2,3) x1, y1 (7,6) x2, y2На графике мы посчитали рост на 3,3. Подъем также можно найти, вычтя y-координаты y-координаты точек.
у2-у16-33у2-у16-33Мы посчитали серию 5,5. Прогон также можно найти, вычтя x-координаты. X-координаты.
х2-х17-25х2-х17-25| Мы знаем | м = стояк |
| Так | м = 35 м = 35 |
| Перепишем подъем и бег, введя координаты. | м = 6−37−2м = 6−37−2 |
| Но 6 — координата yy второй точки, y2y2 и 3 — координата yy первой точки y1y1. Итак, мы можем переписать рост, используя индексную запись. | м = y2 − y17−2m = y2 − y17−2 |
| Также 7 — координата xx второй точки, x2x2 и 2 — координата xx первой точки x2x2. Итак, мы перепишем прогон, используя индексную нотацию. | м = y2 − y1x2 − x1m = y2 − y1x2 − x1 |
Мы показали, что m = y2 − y1x2 − x1m = y2 − y1x2 − x1 на самом деле является еще одной версией m = riserun.m = riserun. Мы можем использовать эту формулу, чтобы найти наклон линии, когда у нас есть две точки на линии.
Формула уклона
Наклон линии между двумя точками (x1, y1) (x1, y1) и (x2, y2) (x2, y2) равен
m = y2 − y1x2 − x1m = y2 − y1x2 − x1Скажите себе формулу, чтобы помочь вам ее запомнить:
Наклон равен второй точке минус первой точки Наклон равен второй точке минус первой точки x второй точки минус x первой точки. x второй точки минус x первой точки.Манипулятивная математика
Выполнение упражнения по манипулятивной математике «Уклон линий между двумя точками» поможет вам лучше понять, как найти наклон линии между двумя точками.
Пример 11.38
Найдите наклон прямой между точками (1,2) (1,2) и (4,5). (4,5).
Решение
| Мы вызовем (1,2) (1,2) пункт №1 и (4,5) (4,5) пункт №2. | (1,2) x1, y1 и (4,5) x2, y2 (1,2) x1, y1 и (4,5) x2, y2 |
| Используйте формулу наклона. | м = y2 − y1x2 − x1m = y2 − y1x2 − x1 |
| Подставьте значения в формулу наклона: | |
| yy второй точки минус yy первой точки | м = 5−2×2 − x1m = 5−2×2 − x1 |
| xx второй точки минус xx первой точки | м = 5-24-1 м = 5-24-1 |
| Упростим числитель и знаменатель. | м = 33 м = 33 |
| м = 1 м = 1 |
Давайте подтвердим это, посчитав наклон на графике.
Подъем 33 и разбег 3,3, поэтому
м = стояк = 33м = 1м = подъемник = 33м = 1
Попробовать 11,74
Найдите наклон прямой, проходящей через заданные точки: (8,5) (8,5) и (6,3). (6,3).
Попробовать 11,75
Найдите наклон прямой, проходящей через заданные точки: (1,5) (1,5) и (5,9). (5,9).
Как мы узнаем, какую точку назвать №1, а какую — №2? Давайте снова найдем наклон, на этот раз поменяв названия точек, чтобы посмотреть, что произойдет.Поскольку теперь мы будем считать пробег справа налево, он будет отрицательным.
| Мы позвоним в (4,5) (4,5) пункт №1 и (1,2) (1,2) пункт №2. | (4,5) x1, y1 и (1,2) x2, y2 (4,5) x1, y1 и (1,2) x2, y2 |
| Используйте формулу наклона. | м = y2 − y1x2 − x1m = y2 − y1x2 − x1 |
| Подставьте значения в формулу наклона: | |
| yy второй точки минус yy первой точки | м = 2−5×2 − x1m = 2−5×2 − x1 |
| xx второй точки минус xx первой точки | м = 2-51-4 м = 2-51-4 |
| Упростим числитель и знаменатель. | м = −3−3м = −3−3 |
| м = 1 м = 1 |
Наклон остается неизменным независимо от того, в каком порядке мы используем точки.
Пример 11.39
Найдите наклон прямой, проходящей через точки (−2, −3) (- 2, −3) и (−7,4). (- 7,4).
Решение
| Мы назовем (−2, −3) (- 2, −3) точкой №1 и (−7,4) (- 7,4) точкой №2. | (−2, −3) x1, y1 и (−7,4) x2, y2 (−2, −3) x1, y1 и (−7,4) x2, y2 |
| Используйте формулу наклона. | м = y2 − y1x2 − x1m = y2 − y1x2 − x1 |
| Заменить значения | |
| yy второй точки минус yy первой точки | м = 4 — (- 3) x2 − x1m = 4 — (- 3) x2 − x1 |
| xx второй точки минус xx первой точки | м = 4 — (- 3) −7 — (- 2) м = 4 — (- 3) −7 — (- 2) |
| Упростить. | м = 7-5 м = 7-5 |
| м = −75 м = −75 |
Подтвердим это на представленном графике.
м = райзерунм = -75м = -75м = райзерунм = -75м = -75
Попробовать 11,76
Найдите наклон прямой, проходящей через пару точек: (−3,4) (- 3,4) и (2, −1). (2, −1).
Попробовать 11,77
Найдите наклон прямой, проходящей через пару точек: (−2,6) (- 2,6) и (−3, −4). (- 3, −4).
Построение линии с заданной точкой и наклоном
В этой главе мы построили линии, нанося точки, используя точки пересечения и распознавая горизонтальные и вертикальные линии.
Другой метод, который мы можем использовать для построения линий, — это метод точечного наклона. Иногда нам дается одна точка и наклон линии вместо ее уравнения. Когда это происходит, мы используем определение наклона, чтобы нарисовать график линии.
Пример 11.40
Изобразите линию, проходящую через точку (1, −1) (1, −1) с наклоном m = 34.m = 34.
Решение
Постройте заданную точку (1, −1). (1, −1).
Используйте формулу наклона m = riserunm = riserun для определения подъема и пробега.
m = 34riserun = 34rise = 3run = 4m = 34riserun = 34rise = 3run = 4 Начиная с точки, которую мы нанесли, отсчитайте подъем и бегите, чтобы отметить вторую точку. Считаем на 33 единицы больше, а на 44 — правильно.
Затем мы соединяем точки линией и рисуем стрелки на концах, чтобы показать продолжение.
Мы можем проверить нашу линию, начав с любой точки и отсчитав 33 и вправо. 4.4. Мы должны добраться до другой точки на линии.
Попробовать 11,78
Постройте линию, проходящую через точку с заданным наклоном:
(2, −2), m = 43 (2, −2), m = 43
Попробуй 11.79
Постройте линию, проходящую через точку с заданным наклоном:
(−2,3), m = 14 (−2,3), m = 14
How To
Постройте линию с учетом точки и наклона.
- Шаг 1. Постройте заданную точку.
- Шаг 2. Используйте формулу наклона для определения подъема и разбега.
- Шаг 3. Начиная с данной точки, отсчитайте подъем и бегите, чтобы отметить вторую точку.
- Шаг 4. Соедините точки линией.
Пример 11.41
Постройте линию с отрезком yy (0,2) (0,2) и наклоном m = −23.m = −23.
Решение
Постройте заданную точку отрезком yy (0,2). (0,2).
Используйте формулу наклона m = riserunm = riserun для определения подъема и пробега.
m = −23riserun = −23rise = –2run = 3m = −23riserun = −23rise = –2run = 3 Начиная с (0,2), (0,2), посчитайте подъем и разбег и отметьте вторую точку.
Соедините точки линией.
Попробуй 11.80
Постройте линию с заданными пересечением и наклоном:
год-точка пересечения 4, m = −524, m = −52
Попробуйте 11,81
Постройте линию с заданным отрезком и наклоном:
xx-точка пересечения −3, m = −34−3, m = −34
Пример 11.42
Изобразите линию, проходящую через точку (−1, −3) (- 1, −3) с наклоном m = 4.m = 4.
Решение
Постройте данную точку.
| Определите подъем и разбег. | м = 4 м = 4 |
| Запишите 4 как дробь. | riserun = 41riserun = 41 |
| подъем = 4 бег = 1 подъем = 4 ход = 1 |
Посчитайте подъем и бег.
Отметьте вторую точку. Соедините две точки линией.
Попробуйте 11,82
Постройте прямую, проходящую через точку (−2,1) (- 2,1) с наклоном m = 3.m = 3.
Попробовать 11,83
Изобразите линию, проходящую через точку (4, −2) (4, −2) с наклоном m = −2.т = -2.
Решите наклонные приложения
В начале этого раздела мы сказали, что в реальном мире есть много применений наклона. Давайте теперь посмотрим на несколько.
Пример 11.43
Уклон крыши здания — это наклон крыши. Знание высоты поля важно в климате с сильным снегопадом. Если крыша слишком плоская, вес снега может вызвать ее обрушение. Какой наклон крыши показан?
Решение
| Используйте формулу наклона. | м = стояк |
| Подставьте значения для подъема и хода. | м = 9 футов 18 футов м = 9 футов 18 футов |
| Упростить. | м = 12 м = 12 |
| Уклон крыши 1212. |
Попробовать 11,84
Найдите заданный уклон и бегите: крыша с подъемом = 14 = 14 и пролетом = 24. = 24.
Попробуйте 11,85
Найдите заданный уклон и бегите: крыша с подъемом = 15 = 15 и пролетом = 36.= 36.
Вы когда-нибудь думали о канализационных трубах, идущих от вашего дома на улицу? Их наклон — важный фактор в том, как они убирают мусор из вашего дома.
Пример 11.44
Канализационные трубы должны иметь уклон 1414 дюймов на фут для правильного отвода воды. Какой требуемый уклон?
Решение
| Используйте формулу наклона. | м = стояк |
| м = -14 дюймов.1 футм = -14 дюймов. 1 фут | |
| м = -14 дюймов 1 футм = -14 дюймов 1 фут | |
| Преобразование 1 фут в 12 дюймов. | м = -14 дюймов. 12 дюймов. М = -14 дюймов. 12 дюймов. |
| Упростить. | м = -148 м = -148 |
| Уклон трубы −148. −148. |
Попробуй 11,86
Найдите уклон трубы: труба имеет уклон 1313 дюймов на фут.
Попробуй 11.87
Найдите уклон трубы: труба имеет уклон 3434 дюйма на ярд.
Раздел 11.4. Упражнения
Практика ведет к совершенству
Использование географических досок для моделирования уклона
В следующих упражнениях найдите уклон, смоделированный на каждой геодлане.
204. 206.В следующих упражнениях моделируйте каждый уклон. Нарисуйте картинку, чтобы показать свои результаты.
Найдите наклон линии по ее графику
В следующих упражнениях найдите наклон каждой показанной линии.
216. 218. 220. 222. 224. 226. 228. 230.Найдите наклон горизонтальной и вертикальной линий
В следующих упражнениях найдите наклон каждой прямой.
Используйте формулу наклона, чтобы найти наклон линии между двумя точками
В следующих упражнениях используйте формулу наклона, чтобы найти наклон линии между каждой парой точек.
245.(−3,3), (2, −5) (- 3,3), (2, −5)
246.(−2,4), (3, −1) (- 2,4), (3, −1)
247.(-1, -2), (2,5) (-1, -2), (2,5)
248.(−2, −1), (6,5) (- 2, −1), (6,5)
249.(4, −5), (1, −2) (4, −5), (1, −2)
250.(3, −6), (2, −2) (3, −6), (2, −2)
Построение линии с учетом точки и наклона
В следующих упражнениях построение линии с учетом точки и наклона.
251.(1, −2); m = 34 (1, −2); m = 34
252.(1, -1); m = 12 (1, -1); m = 12
253.(2,5); m = −13 (2,5); m = −13
254.(1,4); m = −12 (1,4); m = −12
255.(-3,4); м = -32 (-3,4); м = -32
256.(−2,5); m = −54 (−2,5); m = −54
257.(-1, -4); м = 43 (-1, -4); м = 43
258.(−3, −5); m = 32 (−3, −5); m = 32
259.(0,3); m = −25 (0,3); m = −25
260.(0,5); m = −43 (0,5); m = −43
261.(−2,0); m = 34 (−2,0); m = 34
262.(-1,0); m = 15 (-1,0); m = 15
Решите приложения уклона
В следующих упражнениях решите эти приложения уклона.
267.Уклон крыши Достаточно простой способ определить уклон — взять 12-дюймовый 22-дюймовый уровень и установить его одним концом на поверхности крыши. Затем возьмите рулетку или линейку и измерьте расстояние от другого конца уровня до поверхности крыши. Вы можете использовать эти измерения для расчета уклона крыши. Какой уклон крыши на этой картинке?
268.Какой наклон крыши показан?
269.Уклон дороги Уклон дороги местного значения 6%.6%. Уклон дороги — это ее уклон, выраженный в процентах.
- ⓐ Найдите уклон дороги в виде дроби, а затем упростите дробь.
- Ⓑ Какой подъем и спуск будет отражать этот уклон или уклон?
Уровень шоссе Местная дорога поднимается на 22 фута на каждые 5050 футов шоссе.
- ⓐ Какой уклон у трассы?
- Ⓑ Уклон автомагистрали — это ее уклон, выраженный в процентах. Какой уровень у этой трассы?
Повседневная математика
271.Пандус для инвалидных колясок Правила для пандусов для инвалидных колясок требуют подъема максимум на 11 дюймов для бега длиной 1212 дюймов.
- ⓐ Какой пролет должен иметь пандус, чтобы выдержать подъем на 24 дюйма и 34 дюйма до двери?
- Ⓑ Нарисуйте модель этого пандуса.
Пандус для инвалидных колясок Подъем на 1 дюйм2 дюйма для бега на 16 дюймов и 26 дюймов упрощает подъем по пандусу для водителя-коляски.
- ⓐ Какой пролет должен иметь пандус, чтобы легко выдерживать 24-дюймовый 34-дюймовый подъем двери?
- ⓑ Нарисуйте модель этого пандуса.
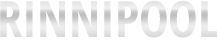
 При выставлении труб располагаете их так, чтобы пузырек оказался в нужном положении.
При выставлении труб располагаете их так, чтобы пузырек оказался в нужном положении.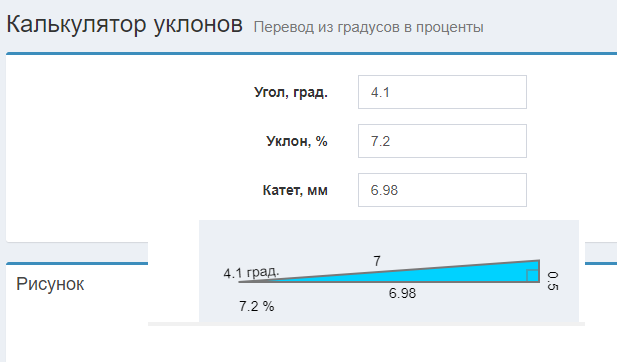

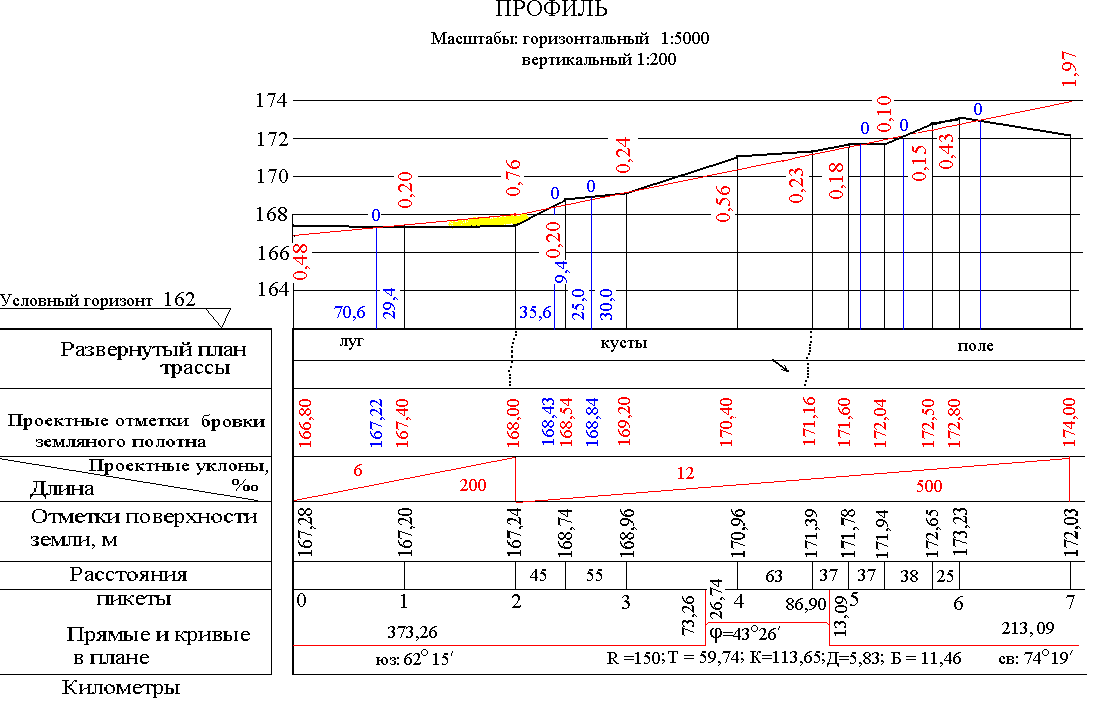 Максимальное расстояние – до 6 м. Наклон должен быть 1 к 20.
Максимальное расстояние – до 6 м. Наклон должен быть 1 к 20.